ЛИНЕЙНЫЕ ОДНОРОДНЫЕ СИСТЕМЫ

Определение.Система m уравнений с n неизвестными вида :

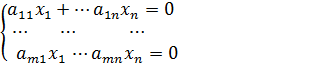(1)

называется линейной однородной системой.

Следуя формулам Крамера, можно сделать вывод:

1). 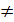0, m=n 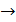система имеет единственное нулевое решение.

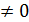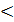2). , m n 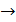система имеет бесчисленное множество решений и среди этих решений могут быть и ненулевые.

Теорема. Для того , чтобы система (1) имела ненулевое решение необходимо и достаточно , чтобы её определитель = 0.

Доказательство необходимости.

Пусть система (1) имеет ненулевое решение , но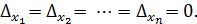

По формулам Крамера имеем:

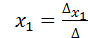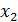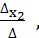
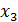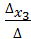
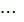
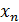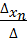, = = = , так как есть ненулевое решение, предположим , что э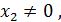то то 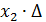= 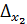, а это возможно только тогда, когда .

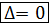Доказательство достаточности.

Пусть = 0 , тогда в формулах Крамера , .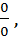

Возьмём r(A) < n и по теореме Кронекера – Капелли система (1) имеет бесчисленное множество решений в том числе и ненулевое.

Вывод.Однородная система уравнений всегда совместна и имеет ненулевое решение только тогда, когда определитель системы равен нулю .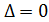

Пример.Решить систему уравнений.

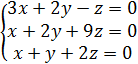
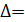
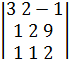= 0 . →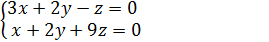

Ранг матрицы последней системы равен 2-м, а число неизвестных равно 3-м, поэтому , следуя теореме Кронекера – Капелли, 3-2=1 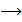свободное неизвестное . Систему перепишем так: 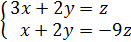и решаем её по формулам Крамера . Для этого найдём 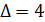, 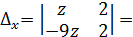2z+18z=20z, =

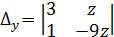=-27z-z=-28z. X = 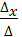= = 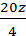5z ; Y = = .

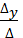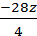Ответ.X = 5z; Y = -7z, где z любое число.