Прямая на плоскости.
Аналогично тому, как выводились канонические уравнения прямой в пространстве выводятся канонические уравнения прямой на плоскости.
| М (х, у) |
| l=(m, n) |
| а |
| М0(х0, у0) |
М0М ║l. Отсюда следует, что 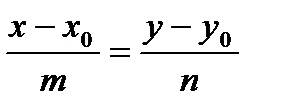 - каноническое уравнение прямой на плоскости, где l=(m, n) - направляющий вектор прямой.
- каноническое уравнение прямой на плоскости, где l=(m, n) - направляющий вектор прямой.
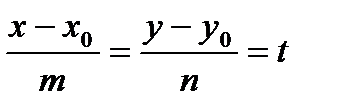 .
.
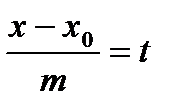
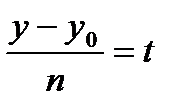 .
.
x= mt+ x0
y= nt+ y0 - параметрические уравнения прямой на плоскости.
| M(x, y) |
| l |
| M2(x2, y2) |
| М1(x1, y1) |
| а |
M1M║M1M2. Отсюда следует, что 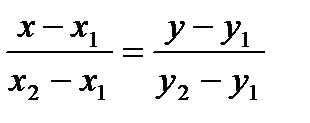 - уравнение прямой через две точки.
- уравнение прямой через две точки.
Если в каноническом уравнении 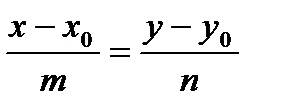 знаменатели m≠0, n≠0, то можно освободиться от знаменателей:
знаменатели m≠0, n≠0, то можно освободиться от знаменателей:
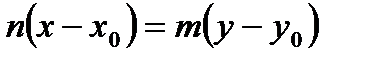 ,
, 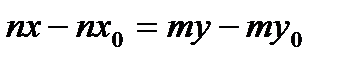 ,
, 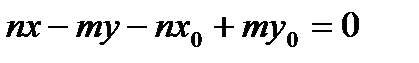 .
.
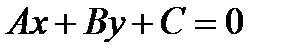 -общее уравнение прямой на плоскости.
-общее уравнение прямой на плоскости.
N= (A, B) - нормаль, перпендикулярная прямой.
Проверка: N= (A, B)= (n, -m), l= (m, n), N•l= m· n- n· m= 0.
⇒ N ^ l. Отсюда следует, что N ^ прямой.
| l= (m, n) |
| N=(A, B) |
Исследуем общее уравнение:
1) А=0, B и С≠ 0, т.е. нет х. Прямая параллельна ОХ.
| x |
| у |
| а |
y= const - уравнение прямой параллельной оси ОХ.
2) В=0, А и С≠ 0, т.е. нет у. Прямая параллельна ОУ.
| у |
| х |
| а |
х= const - уравнение прямой параллельной оси ОУ.
3) С=0, А и В ≠ 0: Ах+Ву=0, т.е. т. О(0, 0) принадлежит прямой. Прямая проходит через начало координат.
| у |
| х |
| а |
4) у=0 - уравнение оси ОХ. х=0 - уравнение оси ОУ.
Пусть прямая отсекает на координатных осях отрезки: a - на оси ОХ и b - на оси ОУ.
| A(a, 0) |
| В(0, b) |
| b |
| у |
| х |
| а |
Прямая проходит через две точки A(a, 0) и В(0, b).
Уравнение: 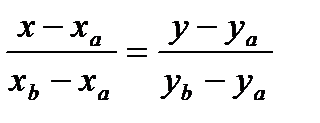 .
.
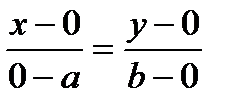 ,
, 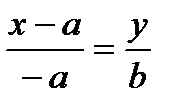 ,
,
b(x-a)= -ay, bx- ab+ ay=0, bx+ ay- ab=0, bx+ ay= ab│: ab,
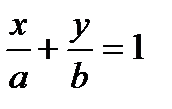 - уравнение прямой в отрезках.
- уравнение прямой в отрезках.
Если в каноническом уравнении 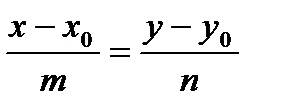 , m≠ 0, то выразим у:
, m≠ 0, то выразим у:
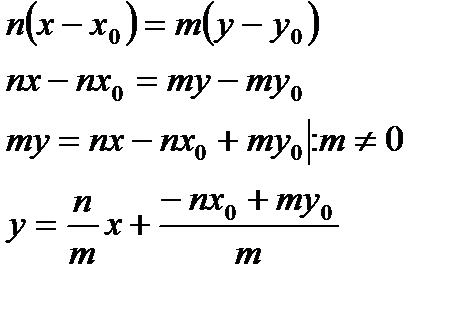
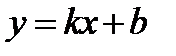 - уравнение прямой с угловым коэффициентом (k).
- уравнение прямой с угловым коэффициентом (k).
Выясним смысл k и b.
Из треугольника: tg α= 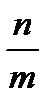 , tg α= k.
, tg α= k.
Угловой коэффициент прямой равен тангенсу угла наклона прямой к положительному направлению оси ОХ.
Так как y(0)=b, то b - отрезок, отсекаемой прямой на оси ОУ.
Через любую точку плоскости проходит бесконечное множество прямых.
Такое множество прямых, проходящих через точку, называется пучком прямых.
Уравнение пучка прямых: 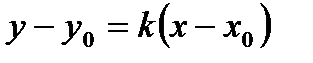 .
.
Задавая различные значения угловых коэффициентов k можно выбирать различные прямые из пучка.
Пример. Вывести формулу для вычисления расстояния от точки до прямой 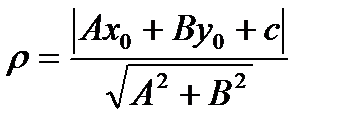 .
.
Дата добавления: 2016-06-05; просмотров: 1753;











