Взаимное расположение прямых в пространстве.

1) Прямая (1) c направляющим вектором l₁= (m₁, n₁, p₁) ║ прямой (2) c направляющим вектором l₂=(m₂, n₂, p₂).

l2

l1

1

l₁ ║ l₂. Отсюда следует, что 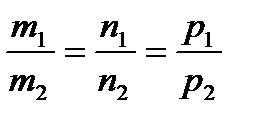- условие параллельности двух прямых в пространстве.

2) Прямая (1) ^ прямой (2).

l2

l1

l₁ ^ l₂. Отсюда следует: l₁• l₂=0.

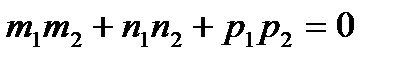- условие перпендикулярности двух прямых в пространстве.

3) Угол между двумя прямыми - это угол между их направляющими векторами.

φ

l1

l2

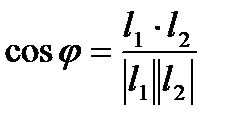- угол между прямыми.

Взаимное расположение прямой и плоскости в пространстве.

Возьмем в пространстве плоскость α с уравнением ,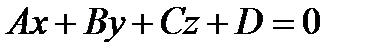

N= (A, B, C), и прямую а с уравнением 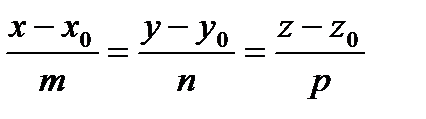, l= (m; n; p).

Возможны следующие случаи расположения:

1) Прямая ^ плоскости.

N║l: 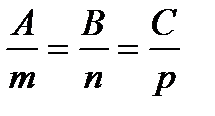- условие перпендикулярности прямой и плоскости.

2) Прямая ║ плоскости.

N ^ l. N•l = 0: Am + Bn + Cp= 0 - условие параллельности прямой и плоскости.

3) Прямая лежит в плоскости.

N ^ l, т. М₀ на прямой Є плоскости.

N•l = 0, координаты т. М₀ удовлетворяют уравнению плоскости.

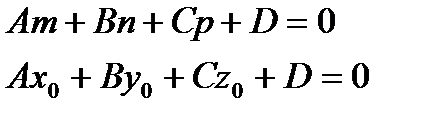- условие принадлежности прямой к плоскости.

4) Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость.

; .

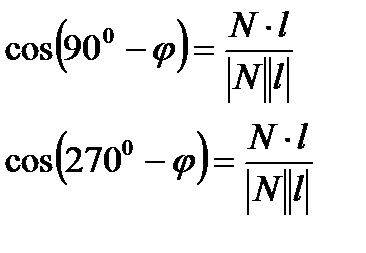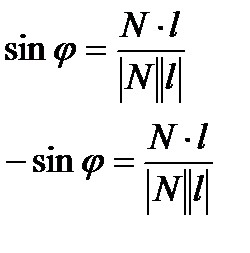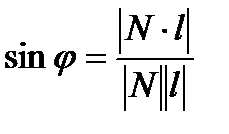- угол между прямой и плоскостью в пространстве.