Векторное произведение двух векторов.
Определение: Векторным произведением a´b векторов a и b называется третий вектор с, обладающий следующими свойствами:
1° │с│=│a│·│b│·sin φ, где Ðj= a,b;
2° вектор c ^ a, c ^b, т.е. с ^ плоскости, в которой лежат вектора а и b;
3° кратчайший поворот от вектора a к b, видимый с конца вектора с будет против часовой.
Свойства векторного произведения:
1° антикоммутативность: a´b= - b´a.
a´b= с, b´a= -с.
2° (λa)´b= λ (a´b).
3° a´(b + с)= a´b + a´с.
4° a ´ а= 0.
│ a ´ а │=│a│·│а│sin 0°= 0. Отсюда следует, что a ´ а= 0.
Векторные произведения координатных ортов.
| i |
| k |
| j |
Если первый орт умножить векторно на второй орт, то по стрелке получим третий орт, причем взятый с «+», если поворот против часовой стрелки, и берется с «-», если по часовой стрелке.
i´j= k,
i´k= -j,
j´k= i,
j´i= -k,
i´i= 0.
Векторное произведение в координатной форме.
a´b= (axi + ayj + azk)×( bxi + byj + bzk)= ax bx i× i + ax by i× j + ax bz i ×k +
+ay bx j×i + ay by j×j + ay bz j×k + az bx k×i + az by k× j + az bz k×k=
= ax by k – ax bz j- -ay bx k+ ay bz i+ az bx j - az by i=
= i(ay bz - azby )- j( ax bz - az bx)+ k(ax by - ay bx )=
=i 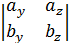 - j
- j 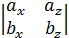 + k
+ k 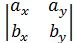 .
.
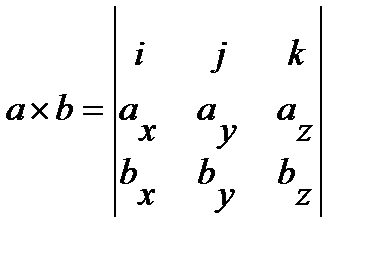 .
.
Дата добавления: 2016-06-05; просмотров: 2379;











