Аналитическая геометрия. Прямая и плоскость
Параметрические уравнения прямой в 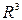
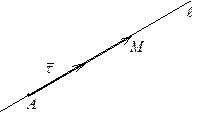
|
Пусть точка 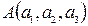 принадлежит прямой
принадлежит прямой 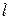 и ненулевой вектор
и ненулевой вектор 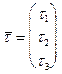 лежит на прямой
лежит на прямой 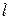 .Тогда можно составить систему уравнений
.Тогда можно составить систему уравнений
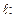 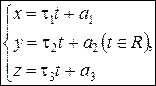
| (1) |
которая называется параметрическими уравнениями прямой в 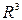 по точке
по точке 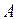 и вектору
и вектору 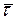 . Число
. Число 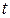 является в уравнениях (1) параметром, могущим принимать любое действительное значение. Вектор
является в уравнениях (1) параметром, могущим принимать любое действительное значение. Вектор 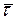 (как и любой вектор, параллельный прямой
(как и любой вектор, параллельный прямой 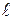 ) называют направляющим вектором прямой
) называют направляющим вектором прямой 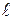 .
.
Пример 1. Запишем уравнения прямой, проходящей через точку 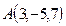 и вектор
и вектор 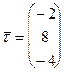 . Подставив имеющиеся данные в уравнение (1), получим:
. Подставив имеющиеся данные в уравнение (1), получим:
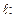 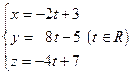 . .
| (2) |
Пример 2. Записать уравнения прямой, проходящей через точки 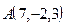 и
и 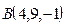 .
.
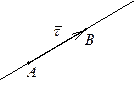
|
Ясно, что направляющий вектор для 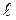 можно задать так:
можно задать так:
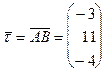
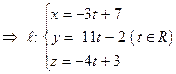 .
.
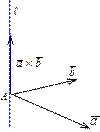
Пример 3. Записать уравнение прямой, проходящей через точку 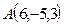 перпендикулярно векторам
перпендикулярно векторам 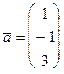 и
и 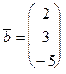 .
.
|
Принимая во внимание теорему о векторном произведении векторов, направляющий вектор для 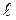 можно вычислить следующим образом:
можно вычислить следующим образом:
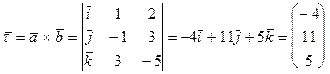 .
.
Следовательно, 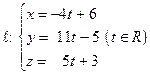 .
.
Выразив параметр 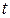 из каждого уравнения системы (1), получим каноническое уравнение прямой прямой
из каждого уравнения системы (1), получим каноническое уравнение прямой прямой 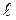 в
в 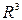 по точке
по точке 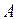 и вектору
и вектору 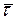 :
:
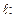 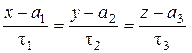 . .
| (3) |
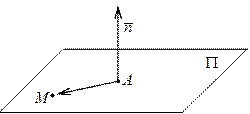
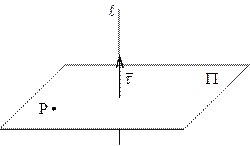
Уравнение плоскости по точке и нормальному вектору
|
Пусть дана точка 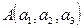 , принадлежащая плоскости
, принадлежащая плоскости 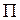 , и ненулевой вектор
, и ненулевой вектор 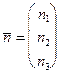 , ортогональный этой плоскости.
, ортогональный этой плоскости.
Составим уравнение плоскости. Для этого рассмотрим на плоскости 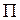 "текущую" точку
"текущую" точку 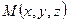 с переменными координатами
с переменными координатами 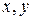 и
и 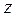 . Наложим на переменные
. Наложим на переменные 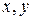 и
и 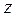 условие, которое, с одной стороны, даст возможность точке
условие, которое, с одной стороны, даст возможность точке 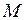 попасть в любую точку плоскости
попасть в любую точку плоскости 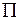 и, с другой стороны, не позволит точке
и, с другой стороны, не позволит точке 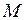 выйти за пределы этой плоскости. Полученное соотношение и будет представлять собой уравнения плоскости
выйти за пределы этой плоскости. Полученное соотношение и будет представлять собой уравнения плоскости 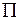 . Имеем цепочку равносильностей:
. Имеем цепочку равносильностей:
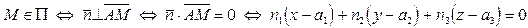 .
.
Уравнение
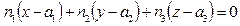
| (4) |
называется уравнением плоскости по точке 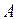 и нормальному вектору
и нормальному вектору 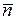 (термины "нормальный вектор", "ортогональный вектор", "перпендикулярный вектор" означают одно и то же). Если в полученном уравнении провести обычные алгебраические преобразования (раскрытие скобок и приведение подобных), то получим уравнение вида:
(термины "нормальный вектор", "ортогональный вектор", "перпендикулярный вектор" означают одно и то же). Если в полученном уравнении провести обычные алгебраические преобразования (раскрытие скобок и приведение подобных), то получим уравнение вида:
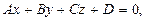
которое называют общим уравнением плоскости.
Пример 4. Запишем уравнение плоскости, проходящей через точку 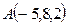 и имеющей нормальный вектор
и имеющей нормальный вектор 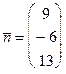 . По формуле (4) имеем:
. По формуле (4) имеем:
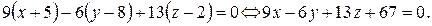
Уравнение плоскости по точке и двум векторам
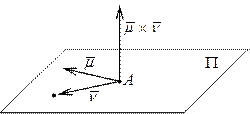
|
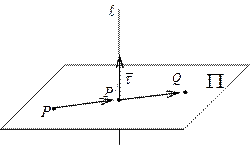
Пусть дана точка 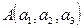 , принадлежащая плоскости П, и два линейно независимых (неколлинеарных) вектора
, принадлежащая плоскости П, и два линейно независимых (неколлинеарных) вектора 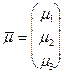 и
и 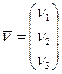 , лежащих в этой плоскости. Составим её уравнение.
, лежащих в этой плоскости. Составим её уравнение.
Очевидно, в качестве нормального вектора можно выбрать вектор 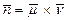 . Взяв текущую точку
. Взяв текущую точку 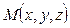 и применяя рассуждения предыдущего пункта, получаем:
и применяя рассуждения предыдущего пункта, получаем:
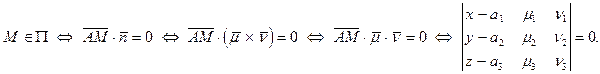 Уравнение
Уравнение
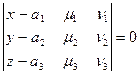
| (5) |
Называется уравнением плоскости по точке 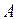 и двум векторам
и двум векторам 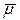 и
и 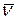 .
.
Пример5. Доказать, что прямые 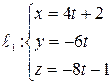 и
и 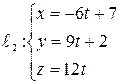 параллельны, но не совпадают, и записать уравнение плоскости, проходящей через
параллельны, но не совпадают, и записать уравнение плоскости, проходящей через 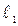 и
и 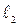 .
.
1)Направляющие векторы данных прямых соответственно равны 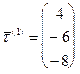 и
и 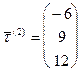 . Так как отношения соответствующих координат равны
. Так как отношения соответствующих координат равны 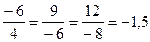 , то
, то 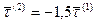 , то есть эти векторы линейно зависимы (коллинеарны). Значит,
, то есть эти векторы линейно зависимы (коллинеарны). Значит, 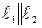 .
.
2)Теперь чтобы доказать, что 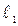 и
и 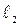 не совпадают, достаточно проверить, что точка, лежащая на одной прямой, не лежит на другой. Положив
не совпадают, достаточно проверить, что точка, лежащая на одной прямой, не лежит на другой. Положив 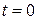 в первой системе, получаем точку
в первой системе, получаем точку 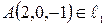 . Покажем, что
. Покажем, что 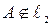 . Подставим координаты точки
. Подставим координаты точки 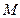 во вторую систему:
во вторую систему: 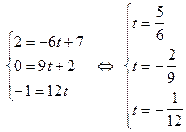 . Эта система противоречива, поэтому
. Эта система противоречива, поэтому 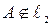 .
.

|
3) Запишем уравнение плоскости, проходящей через 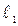 и
и 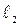 . Положив
. Положив 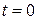 в параметрических уравнениях прямой
в параметрических уравнениях прямой 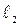 , получим точку
, получим точку 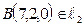 . Возьмем
. Возьмем 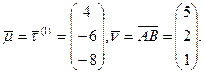 По формуле (5) получаем искомое уравнение плоскости:
По формуле (5) получаем искомое уравнение плоскости:
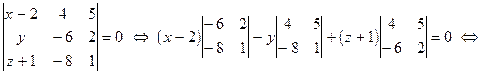
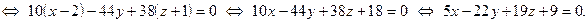
Решим ещё несколько задач на прямую и плоскость в пространстве.
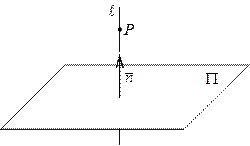
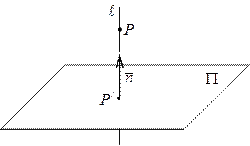
Пример 6. Найти точку 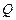 , симметричную точке
, симметричную точке 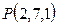 относительно плоскости
относительно плоскости 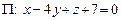 .
.
|
1)Запишем уравнение прямой 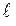 , проходящей через точку
, проходящей через точку 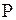 перпендикулярно плоскости
перпендикулярно плоскости 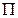 . Так как в качестве направляющего вектора
. Так как в качестве направляющего вектора 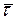 прямой
прямой 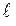 можно взять нормальный вектор плоскости
можно взять нормальный вектор плоскости
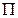 -
- 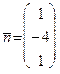 , то параметрические уравнения
, то параметрические уравнения 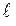 имеют вид:
имеют вид: 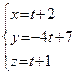 .
.
|
2)Найдем точку пересечения 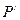 прямой
прямой 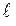 и плоскости
и плоскости 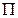 . Для этого решим систему уравнений:
. Для этого решим систему уравнений:
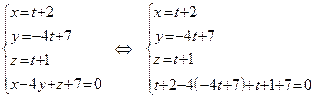 .
.
Таким образом, 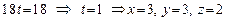 То есть,
То есть, 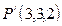 .
.
|
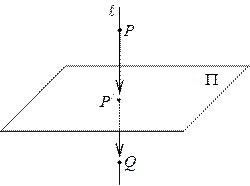
3) Пусть 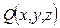 – точка, симметричная точке P относительно плоскости
– точка, симметричная точке P относительно плоскости 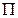 . Так как
. Так как 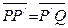 , то
, то 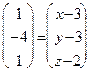
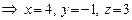 . То есть
. То есть 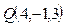 .
.
|
Пример 7. Найти точку Q, симметричную точке 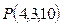 относительно прямой
относительно прямой 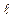 :
: 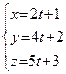 .
.
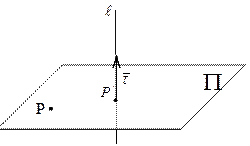
1) Запишем уравнение плоскости 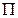 , проходящей через точку P перпендикулярно прямой
, проходящей через точку P перпендикулярно прямой 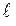 . Так как в качестве нормального вектора плоскости
. Так как в качестве нормального вектора плоскости 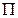 можно взять направляющий вектор прямой
можно взять направляющий вектор прямой 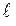 , который равен
, который равен 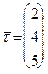 , то по формуле (4):
, то по формуле (4): 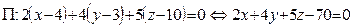 .
.
|
2)Найдем точку пересечения 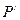 прямой
прямой 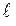 и плоскости
и плоскости 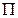 . Решим систему уравнений:
. Решим систему уравнений:
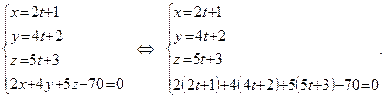 Получаем:
Получаем: 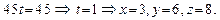 То есть
То есть 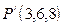 .
.
|
2) Пусть 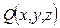 – точка, симметричная точке
– точка, симметричная точке 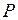 относительно прямой
относительно прямой 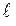 . Так как
. Так как 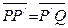 , то
, то 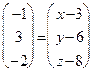
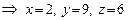 . То есть
. То есть 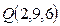 .
.
Прямая в 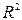
Общим уравнением прямой на плоскости называется уравнение вида:
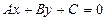
| (6) |
Если 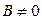 , то разрешая (6) относительно
, то разрешая (6) относительно 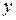 , получим уравнение прямой с угловым коэффициентом:
, получим уравнение прямой с угловым коэффициентом:
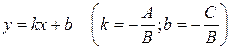 . .
| (7) |
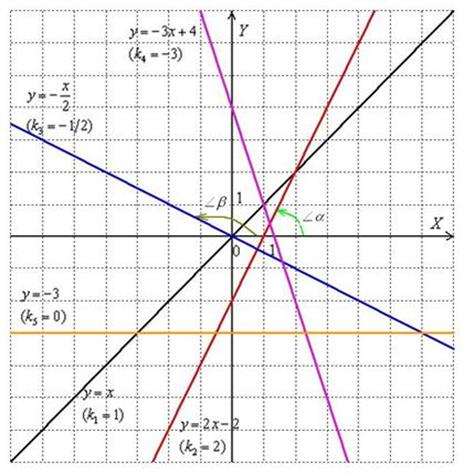
Таким образом, геометрический смысл числа 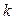 состоит в том, что
состоит в том, что 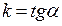 , где
, где 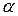 – угол, образованный прямой с положительным направлением оси
– угол, образованный прямой с положительным направлением оси 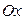 . У параллельных прямых угловые коэффициенты равны (
. У параллельных прямых угловые коэффициенты равны ( 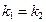 ). У перпендикулярных прямых угловые коэффициенты обратны по величине и противоположны по знаку
). У перпендикулярных прямых угловые коэффициенты обратны по величине и противоположны по знаку 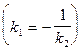 . Уравнение прямой, имеющей угловой коэффициентkи проходящей через точку
. Уравнение прямой, имеющей угловой коэффициентkи проходящей через точку 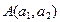 ,записывается в виде:
,записывается в виде:
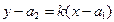 . .
| (8) |
Уравнение прямой, проходящей через две точки 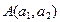 и
и 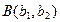 , имеет вид:
, имеет вид: 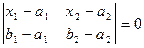 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Пересечение поверхности плоскостью общего положения | | | Интегрирование линейных неоднородных дифференциальных уравнений |
Дата добавления: 2017-11-21; просмотров: 2070;











