Второе свойство. Проекция прямой линии в общем случае есть прямая.

Г Ç a, Г Ç П₁ Þ a₁

Если прямая параллельна направлению проецирования, то она вырождается в точку.

l_C É C, l_C || s, l_C Ç П₁ = C₁; C₁ - точка

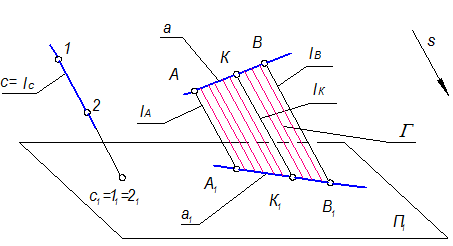
Рис. 1-8

Третье свойство – принадлежности. Если точка принадлежит прямой, то проекция точки

принадлежит проекции прямой, К Î а Þ К₁ Î а₁

Это свойство следует из определения проекции фигуры, как совокупности проекций всех ее точек (см. рис. 1-8)

Четвертое свойство - свойство простого соотношения трех точек. Если точка делит отрезок в некотором отношении, то и проекция этой точки делит отрезок в том же отношении (см. рис. 1-8).

|AK| : |KB| = |A₁K₁| : |K₁B₁|

Пятое свойство. Если прямые в пространстве параллельны, то их проекции ||.

m || n Þ m₁ || n₁, т. к. Г || S (Рис 1-9)

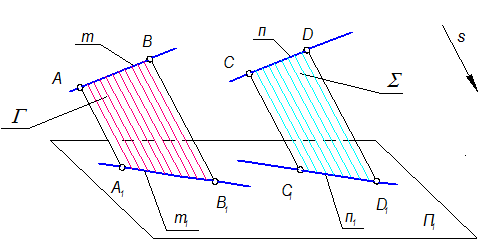
Рис. 1-9

Шестое свойство. Отношение длин отрезков параллельных прямых равно отношению длин их проекций, АВ || СD Þ А₁В₁ || С₁D₁ (Рис 1-9)

Седьмое свойство. Проекция геометрической фигуры не изменяется при параллельном переносе плоскостей проекций: A₁B₁C₁ = A¹B¹C¹

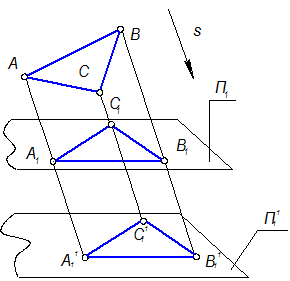
Рис. 1-10

Если П₁ || П₁¹, то А₁А₁¹ = В₁В₁¹ = С₁С₁¹ - как параллельные отрезки, заключенные между параллельными плоскостями, следовательно четырехугольники А₁А₁¹В₁В₁¹ и В₁В₁¹С₁С₁¹ и С₁С₁¹А₁А₁¹ являются параллелограммами, а у параллелограммов параллельные стороны равны. Поэтому DА₁В₁С₁ = А₁¹В₁¹С₁¹

Рассмотренные свойства параллельного проецирования сохраняются при любом направлении проецирования.