Второй тип задач –прямая частного положения и поверхность общего положения

Пример 3. Построить точки пересечения М и N прямой l, перпендикулярной к фронтальной плоскости, с поверхностью пирамиды (рисунок 8-3).

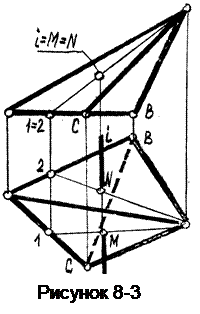Решение задачи начинаем с вида спереди, где прямая вырождается в точку. Точки пересечения, поэтому здесь будут совпадать с вырожденным видом прямой.

Прямая "пронзает" пирамиду в двух ее гранях: ASC и АSВ. Для нахождения точек М и N на виде сверху проведем через эти точки на виде спереди вспомогательные прямые S-1 и S-2 в гранях ASС и ASB соответственно. Пересечение этих вспомогательных прямых на виде сверху с прямой l определит положение точек М и N.

Видимость прямой определяем исходя из пространственного представления.

Пример 4. Построить точки пересечения М и N прямой i, перпендикулярной к фронтальной плоскости, со сферой (рисунок 8-4).

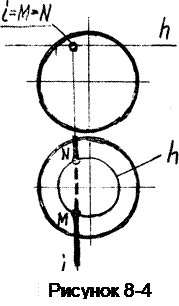Точки пересечения М и N на виде спереди будут совпадать с вырожденным видом прямой i.

Для нахождения их на виде сверху, проведем на поверхности сферы вспомогательную графически простую линию, проходящую через точки М и N,

Такой линией является параллель hсферы (окружность). Пересечение параллели с прямойi на виде сверху определит положение искомых точек. Определяем видимость прямой.

Как видно из рассмотренных задач, в основе построения точек пересечения прямой с поверхностью лежит свойство принадлежности линии и поверхности.

К

Пример 5. Построить точки пересечения горизонтали h с поверхностью сферы (рисунок 8-5).

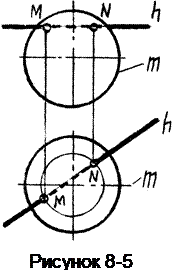Линией на поверхности сферы, конкурирующей с данной прямой, является окружность.

При решении задач следует строить такую конкурирующую линию, которая проецируется на видах как графически простая линия (прямая или окружность) - при этом значительно упрощается решение.

Если в предлагаемой задаче построить вспомогательную линию горизонтально-конкурирующую с прямой h , то эта линия на виде спереди изобразится эллипсом, построение которого довольно сложно.

Решение упрощается, если на сфере построить линию фронтально-конкурирующую с горизонталью h, т.к. в этом случае окружность на виде сверху проецируется без искажения. Точки пересечения окружности с горизонталью будут искомыми.

Видимость прямой определяется исходя из видимости поверхности сферы. На виде сверху видна часть поверхности, лежащая выше экватора, поэтому здесь будет невидима только часть прямой, лежащая между точками М и N .находящаяся внутри поверхности.

На виде спереди видимой будет часть поверхности, которая лежит перед главным меридианом т. Точка М находится перед главным меридианом m, поэтому она на виде спереди видна; участок прямой влево от т.М тоже будет видимым. Точка N, наоборот, невидна; участок вправо от нее до контура сферы тоже невидим.