ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ ОБЩЕГО ПОЛОЖЕНИЯ
Прямой угол между перпендикулярными прямыми общего положения на комплексном чертеже искажается (свойство ортогональной проекции прямого угла).
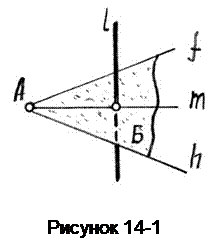Через любую точку пространства можно провести множество прямых, перпендикулярных данной прямой общего положения. Все они будут лежать в плоскости, перпендикулярной этой прямой и только одна из них пересечёт её (рисунок 14-1).
Решение вопроса о перпендикулярности прямых общего положения сводится к перпендикулярности прямой и плоскости. Здесь используется положение о том, что две прямые перпендикулярны только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
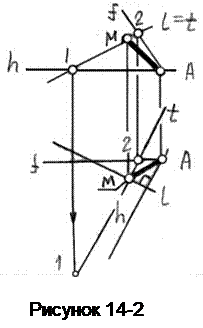
Пример 10. Определить расстояние от точки А до прямой общего положения l (рисунок 14-2).
Для построения прямой, перпендикулярной данной, надо построить сначала плоскость, проходящую через заданную точку и перпендикулярную данной прямой i.
Эту плоскость задаем горизонталью h и фронталью f, проведенными перпендикулярно прямой l.
Затем находим точку пересечения прямой с перпендикулярной ей плоскостью.
Соединив точку пересечения К с точкой А, получим перпендикуляр, опущенный из точки А на прямую l, Определяем его истинную величину.
Пример 11.Определить, перпендикулярны ли прямые m и n(рисунок 14-3).
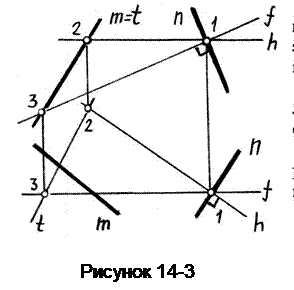Сначала построим плоскость Б перпендикулярную прямой n (плоскость задаем пересекающимися горизонталью и фронталью).
Затем определяем относительное положение прямой т и полученной плоскости Б .
|
В приведенном примере mне перпендикулярна n.
Дата добавления: 2017-11-21; просмотров: 1073;
Поиск по сайту
Узнать еще
- I. ОСНОВНЫЕ ПОЛОЖЕНИЯ
- II. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ДВИЖЕНИЯ
- А теперь рассмотрим основные положения 3 методики.
- А) Система общего образования
- А. Общего пользования – поступает от разных поставщиков.
- Агрегатная форма общего индекса
- Агрессивное поведение. Основные положения
- Административная юстиция в странах системы общего права
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
