Формула Байеса (формула проверки гипотез)

Пусть событие А уже произошло, тогда вероятность того, что появилось событие Н_i, где i=1,2,3,…n, равна:

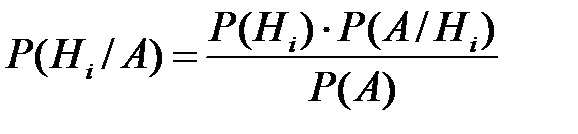(Формула Байеса),

где P(A) можно найти по формуле полной вероятности.

Доказательство:

Из Т2.1. имеем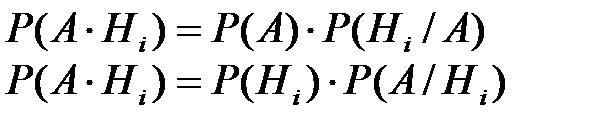

Приравнивая правые части равенств, получаем: 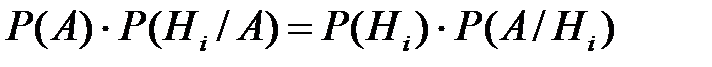. Отсюда имеем .

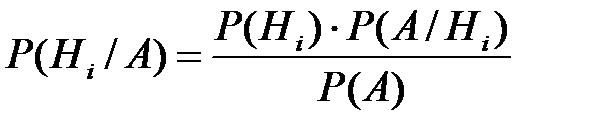Формула Байеса, по которой вычисляется апостериорная вероятность лингвистических гипотез, используется в различных лингвистических исследованиях, в том числе, в теории решения задач, применяемой в инженерной лингвистике.

Пример. Имеется английский научно-технический текст общей длиной в 400 тыс. словоупотреблений (около тысячи стандартных страниц). По тематике этот текст распадается на следующие 4 выборки разной длины: радиоэлектроника – 200 тыс. словоупотреблений; автомобилестроение – 100 тыс. словоупотреблений; судовые механизмы – 50 тыс. словоупотреблений; строительные материалы. – 50 тыс.словоупотреблений. Словоформа ‘are’ - множественное число настоящего времени глагола ‘to be’ ‘быть’ употреблена …

в 1-й выборке-1610 раз, во 2-й -1273, в 3-й – 469, в 4-й – 346 раз

[Пиотровский, 1977, с. 131]

а) Определить вероятность того, что извлечённое наугад из данного текста словоупотребление будет словоформой ‘are’.

Решение. Событие А = «появилась словоформа ‘are’» может произойти только с одним из 4-х событий, образующих полную группу:

В = «словоформа из текста по радиоэлектронике», С=«словоформа из текста по автомобилестроению», D =«словоформа из текста по судовым механизмам», Е = «словоформа из текста по строительным материалам». Эти события несовместны, следовательно, можно применить формулу полной вероятности: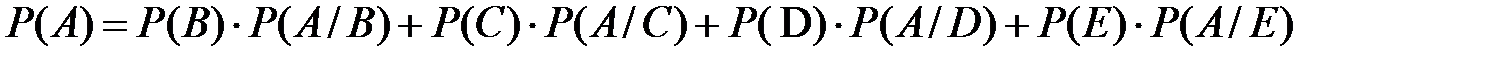

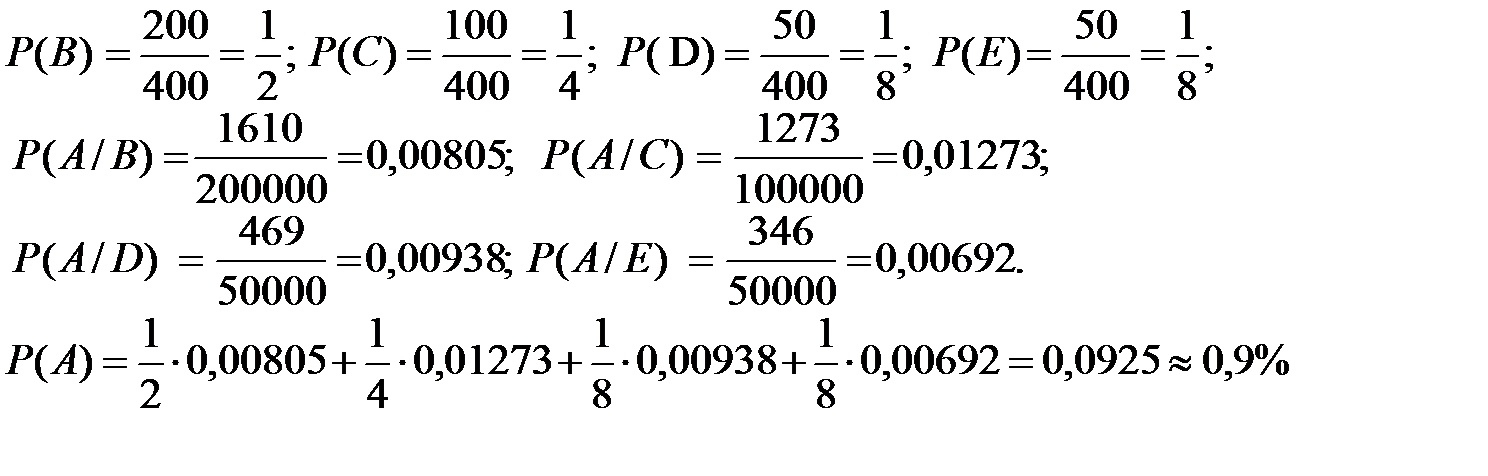
б) Пусть наугад извлечённая словоформа в выборке оказалась глаголом ‘are’. Найти вероятность того, что эта словоформа извлечена из текста по электронике.

Решение. Событие А = «появилась словоформа ‘are’» уже произошло, а надо определить вероятность В при условии, что А произошло.

По формуле Байеса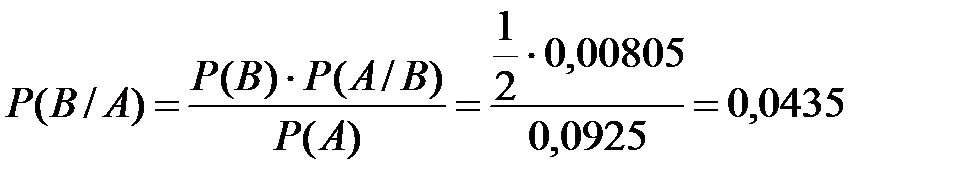

Вероятность, что выбранная словоформа ‘are’ извлечена из текста по электронике, равна 0, 0435

Теорема Бернулли

Пусть производится n независимых одинаковых испытаний.

Событие А в каждом из испытаний может появиться с вероятностью p, и не появиться с вероятностью q=1-p.

Тогда вероятность того, что событие А появится m раз из n находится по формуле:

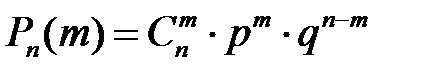– формула Бернулли.

Примером использования теоремы Бернулли может служить повторная выборка согласных (А) и гласных ( 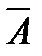) фонем из определённого текста. Предположим, что в некотором тексте длиной в n фонем имеется m гласных и n-m согласных. Требуется определить, что среди извлечённых N фонем ровно x окажутся согласными, причём порядок следования согласной и гласной фонем безразличен.

При составлении алгоритмов пословного машинного перевода и информационного поиска возникают задачи, связанные с прогнозированием появления в сегментах заданной длины определённого числа словоформ, морфем или словосочетаний, принадлежащих к некоторым классам. Формула Бернулли позволяет решать задачи такого типа, при условии, что сохраняется взаимная независимость образующих данный сегмент словоформ.

Пример. [Пиотровский, 1977, с. 153]. Относительная частота появления существительных в подъязыке английской электроники близка к 1/3(априорная вероятность). Примем, что типовым синтаксически оформленным сегментом в английских научно-технических текстах является простое предложение, а также главное и придаточное предложение длиной в 10 словоформ. Считая появление отдельных словоформ в этих сегментах независимыми событиями текста, определить вероятность того, что из 10 словоупотреблений, составляющих типовой сегмент ровно 2 будут существительными.

Решение. Так как появление существительных в типовом сегменте – события независимые, и вероятность появления каждого из существительных одинакова, то можно найти искомую вероятность по формуле Бернулли: 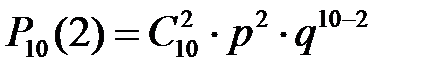, где p=1/3; q=1-1/3=2/3;

.

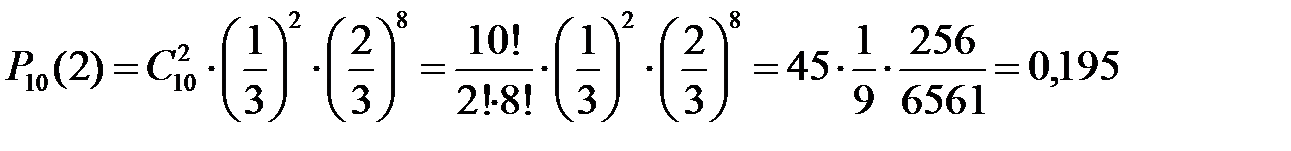Ответ: вероятность появления двух существительных в типовом сегменте английского текста по электронике равна 19,5 %