Статистическое определение вероятности
На практике редко можно найти вероятность события по формуле классической вероятности (из-за невозможности определения числа исходов или доказательства их равновозможности). В этих случаях используют статистическую вероятность события.
Пусть производится 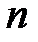 одинаковых независимых испытаний.
одинаковых независимых испытаний.
Событие А появилось в них 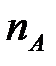 раз (
раз ( 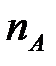 - частота события А).
- частота события А).
Тогда отношение 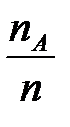 называется относительной частотой события А.
называется относительной частотой события А.
При увеличении количества испытаний 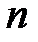 , относительная частота
, относительная частота 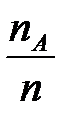 группируется около числа p (сходится по вероятности к р):
группируется около числа p (сходится по вероятности к р):
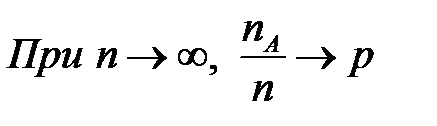
Число p называется статистической вероятностью события А.
Эта закономерность носит название устойчивости относительных частот. Устойчивость относительных частот наблюдается при многократном проведении большого числа одного и того же опыта.
Например, относительная частота глагола «быть» в русской художественной прозе при увеличении объёма исследуемого материала приобретает определённую устойчивость, приближаясь к числу 0,01.
| n (объём выборки) | m (частота глагола «быть») | Относительная частота | n (объём выборки) | m (частота глагола «быть») | Относительная частота |
| 0,000 | 0,010 | ||||
| 0,030 | 0,010 | ||||
| 0,015 | 0,009 | ||||
| 0,008 | 0,010 | ||||
| 0,010 | 0,010 | ||||
| 0,008 | 0,010 | ||||
| 0,009 | 0,011 |
Таблица 1. Относительная частота глагола «быть»
в произведениях Пушкина, Тургенева, Бунина. [22,с.119].
Я. Бернулли в 1713 году доказал теорему, которая носит название «закона больших чисел в форме Бернулли» и объясняет близость относительной частоты к числу р, которое и является истинной вероятностью события А: как бы ни было мало число 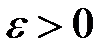 ,
, 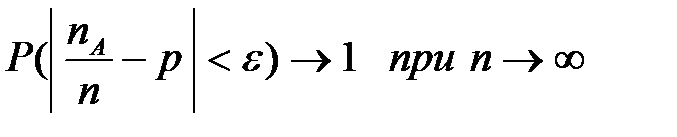 , где р - вероятность события А в каждом отдельном испытании. Говорят, что относительная частота сходится по вероятности к вероятности этого события:
, где р - вероятность события А в каждом отдельном испытании. Говорят, что относительная частота сходится по вероятности к вероятности этого события: 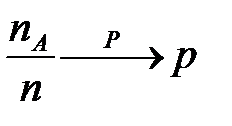
В лингвистике часто за приближённое численное значение статистической вероятности принимается при большом количестве испытаний либо сама относительная частота события А, либо некоторое число, близкое к этой относительной частоте (например, среднее арифметическое относительных частот, полученных из нескольких, достаточно больших серий испытаний). Этот подход имеет практическое значение для прикладных лингвистических исследований, например, при составлении частотных словарей.
Пример. Исследуется частотность употребления частей речи в прозе К. Федина. Взято 10 однородных фрагментов по 500 знаменательных слов каждая. Получены следующие частоты имён существительных: 182, 187, 218, 173, 158, 201, 222, 233, 213, 194. Так как количество испытаний велико (5000 слов), за приближённое значение статистической вероятности р можно взять среднюю частоту появления существительного: 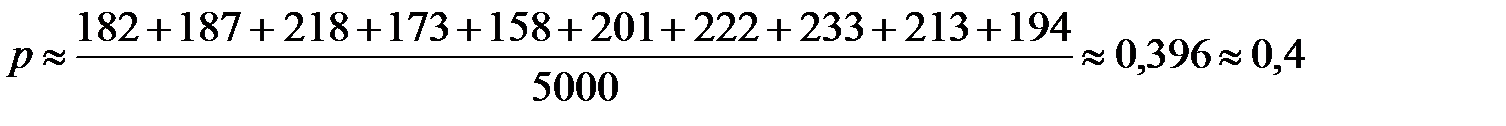
Ответ: Проза Федина характеризуется частым (40%) употреблением существительных, т.е. повествование является предметным.
Дата добавления: 2016-06-05; просмотров: 2180;











