Функция распределения СВХ F(x)
(интегральная функция распределения)
Функция распределения случайной величины Х равна вероятности того, что случайная величина Х примет значение меньшее, чем x, x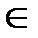 
R
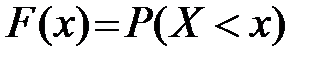X<х
х
Свойства F(x):
а) F(x) – неубывающая, т.е. для всех х, таких, что x2 >х1, верно F(x2)≥F(x1);
б)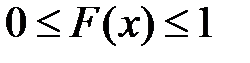 
, т.к. это вероятность;
в) При х→-∞, F(x) →0, т.к. F(-∞)=P(X<-∞)=0;
При х→∞, F(x) →1, т.к. F(∞)=P(X<∞)=1
Для НСВР(a<Х<b)=F(b)-F(a), при a<b
Доказательство:
P(X<b) = P(X<a)+P(a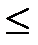 
Х<b) X<a a 
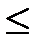Х<b
P(a 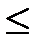Х<b)=P(X<b)- P(X<a)-Р(Х=а) = F(b)-F(a)
т.к. для НСВР(Х=а)=0 а b x
Задача 1. Вероятность появления глагола в произведениях Л.Н. Толстого равна 0,21, а в произведениях А.И. Куприна – 0,15 (статистическая вероятность) (Головин, 1971, с. 14). Из текста каждого автора произвольно выбирают по одному слову. Составить закон распределения случайной величины X – «Количество выбранных глаголов». Найти функцию распределения F(x) и построить её график.
Решение. а) СВ Х может принимать значения 0; 1 или 2. Найдем вероятности их появления. Пусть А - «выбран глагол из произведений Л.Н. Толстого», В - «выбран глагол из произведений А.И. Куприна». Р(А)=0,21, P(B)=0,15, P(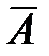 
)=0,79, P( 
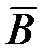)=0,85.
Р(Х=0) =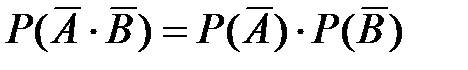 
=0,6715 (А и В независимые события)
P(X=1)=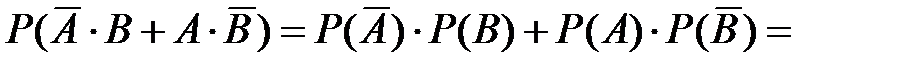 
0,297.
Р(Х=2) = Р(А 
В)=Р(А) 
Р(В)=0,0315.
Заполним таблицу:
| Х | |||
| Р | 0,6715 | 0,297 | 0,0315 |
Проверка: 0,6715+0,297+0,0315=1
Получили закон распределения Х.
б) Найдём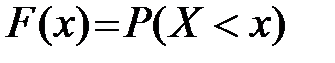 
0 1 2 х
Вероятность того, что значения СВ Х будут меньше, чем
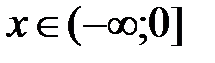равна нулю, т.к. нет таких значений СВ.
Вероятность того, что значения СВ Х будут меньше, чем х (0;1] равна Р(Х=0)=0,6715, т.к. только значение 0 меньше, чем данные х.
Вероятность того, что значения СВ Х будут меньше равна
сумме вероятностей P(X=0) и P(X=1), т.к. Х=0 и Х=1 меньше, чем xиз этого промежутка. F(x) = P(X=0)+P(X=1)= 0,6715+0,297=0,9685.
При х>2 F(x)=P(X=0)+P(X=1)+P(X=2)=1
Тогда функция F(x) будет иметь вид:
| 0,9685 |
| 0,6715 |
| F(x) |
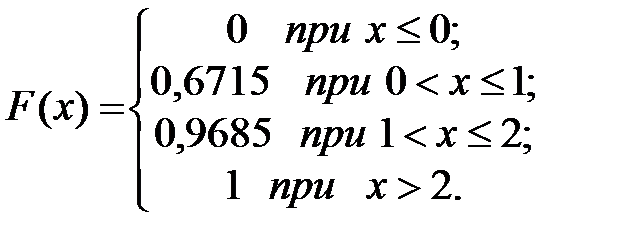
0 1 2 x
Фунция распределения любой ДСВ всегда является разрывной ступенчатой функцией, скачки которой происходят в точках, соответствующих значениям СВ Х. Длина скачка равна вероятности СВ в данной точке.
Для НСВ функция распределения F(x) непрерывна на R.
3.3. Функция плотности вероятности НСВ f(x)
(дифференциальная функция распределения)
Плотностью вероятности f(x) (или плотностью распределения) непрерывной СВ называется первая производная от функции распределения :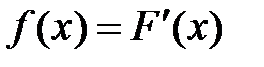 
f(x) характеризует плотность, с которой распределяются значения СВ в данной точке.
Свойства f(x):
| S=1 |
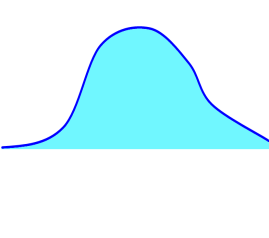а) f(x)≥0, т.к. F(x) – неубывающая;
б) при х→-∞ или х→∞, f(x) →0;
| х |
плотности вероятности и осью х равна 1.
Дата добавления: 2016-06-05; просмотров: 2505;
Поиск по сайту
Узнать еще
- I.1.6 ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. ЗАКОН РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ
- А- передаточная функция при трех разных температурах
- Автокорреляционная функция сигналов
- Автор как функция: М. Фуко
- Алгоритм предварительного распределения ресурсов
- Анализ - функция управления
- АППРОКСИМАЦИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
- Арифметические операции над функциями. Композиция функций
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
