Вероятность произведения событий

Определение. Два события называются независимыми, если вероятность появления одного из них не зависит от того, произошло или нет другое. В противном случае события называются зависимыми.

Определение. События А₁, А₂, ,А_n называются независимыми, если независимы любые комбинации (или произведения) этих событий

Определение. Условной вероятностью события А при условии В называется вероятность происхождения события А, при условии, что В уже произошло. Обозначается P(A/B)

Примеры.

1) На карточках разрезной азбуки написано слово «ФИЛОЛОГИЯ». Последовательно извлекают две карточки без возвращения. Событие В = «1-я карточка с буквой О», событие А = «2-я карточка с буквой О». Найдём условные вероятности события А при условии, что событие В уже произошло и при условии, что событие В не произошло (т.е. произошло событие ): .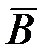

Так как 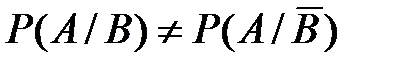,то А и В – зависимые события.

2) Пусть испытание состоит в извлечении карточек и возвращении их обратно. События К = «1-я карточка с буквой О» и D=«2-я карточка с буквой О» являются независимыми, так как появление буквы О на второй извлечённой карточке не зависит от того, появилась или нет буква О при извлечении первой карточки: .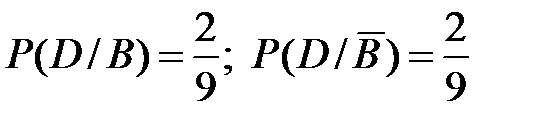

Т.2.1.Вероятность произведения двух зависимыхсобытий равна произведению вероятности одного из этих событий на условную вероятность другого, при условии, что первое уже произошло.

Для нескольких зависимых событий А₁,А₂,…А_n:

Т2.2. Вероятность произведения независимых событий равна произведению их вероятностей

Пример.1. [Пиотровский, 1977, с. 125]. Для расчёта памяти автомата, распознающего устную речь, и построения алгоритма его работы приходится вычислять вероятность совпадения хотя бы одной из словоформ обрабатываемого текста с соответствующей лексемой, заданной в словаре автомата.

а). Выбрано два одинаковых по объёму отрывка текста, из каждого отрывка произвольно выбирается слово. Нужно определить, что хотя бы одно из двух выбранных слов будет местоимением он, если согласно данным частотного словаря, значение статистической вероятности появления местоимения он в тексте равно 0,0099.

Обозначим события: А=«Первое слово - местоимение он»; В=«Второе слово - местоимение он». Тогда событие А+В = «хотя бы одно из двух слов - местоимение он». Так как А и В совместные события, то P(A+B) = 0,0099+0,0099-0,0099 0,0099=0,2.

б). Выбрано десять одинаковых по объёму отрывков текста,

из каждого отрывка произвольно выбирается слово. Найти вероятность события D = «Хотя бы одно из десяти выбранных слов текста будет местоимением он» [22]. Найдём сначала вероятность события 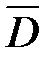= «ни одно из десяти выбранных слов текста не будет местоимением он». 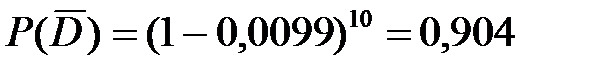– вероятность произведения 10 независимых событий. Тогда 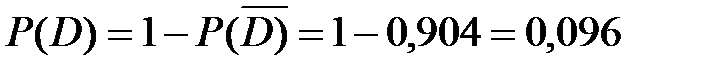(сл. 2)

Пример.2. В лингвистике очень редко имеют дело с независимыми событиями, т.к. вероятность появления букв, фонем, слогов, морфем и т.д. зависит от позиций этих лингвистических объектов в слове, словосочетании, предложении.

Пример. Определите вероятность появления в русских текстах двухбуквенного сочетания «яп» в начале слова, если вероятность появления буквы я в начале слова равна 0,018, а вероятность появления буквы п после начального я составляет 0,001. [данные из 22].

Введём обозначения: А= «первая буква слова – я», В= « вторая буква слова – п», тогда А В= «первая буква слова – я, и одновременно вторая буква – п». Р(А)= 0,018; Р(В/А)=0,001. Так как события А и В –зависимые, то воспользуемся формулой вероятности произведения для зависимых событий: Р(А В)=Р(А) Р(В/А)=0,018 0,001=0,00018.