Классическое определение вероятности
1) Пусть в некотором опыте может произойти n равновозможных, несовместных событий (исходов), причём одно из них обязательно наступит.
2) Интересующее нас событие А наступит, если наступит одно из m (m ≤n) равновозможных, несовместных, событий.
Тогда вероятность события А равна 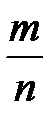 , что записывается в виде
, что записывается в виде 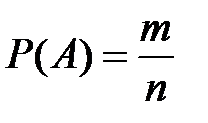 - формула классической вероятности события А,
- формула классической вероятности события А,
m –число событий , благоприятных событию А (из n),
n –числовсего возможных исходов: равновозможных, несовместных, событий.
Свойства вероятности:

Исходя из классического определения вероятности, осуществляется, например, вероятностная обработка частотных словарей отдельных произведений или всего творчества писателя. В этих случаях все словоупотребления, составляющие текст, образуют полную группу равновозможных элементарных событий.
Пример. Текст «Капитанской дочки» А.С.Пушкина состоит из 29343 словоупотреблений. Формы слова «быть» встречаются здесь 430 раз. Найти вероятность появления в тексте «Капитанской дочки» форм слова «быть» [Пиотровский, 1977, с.118].
Введём обозначение: событие А= «появилась форма слова быть». Так как у каждого словоупотребления имеется одинаковая возможность быть выбранным, то выбор любой словоформы – равновозможные события. Для нахождения вероятности события А применим формулу классической вероятности, где n =29343 – число всего равновозможных несовместных событий (исходов), m=430 – число событий, благоприятных событию А. Тогда 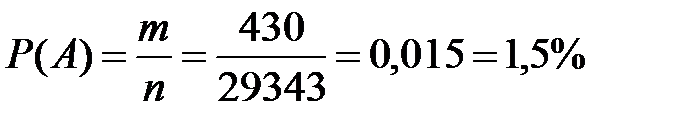 .
.
Вывод: 1,5% всех слов в произведении А.С. Пушкина «Капитанская дочка» составляют формы слова быть, что является отличительной характеристикой данного произведения
Дата добавления: 2016-06-05; просмотров: 1772;











