Бинарная задача проверки простых гипотез

Наиболее просто задача построения оптимального приемника решается для случая амплитудной телеграфии с пассивной паузой, что соответствует принятию решения о том, что передавался символ 0 (сигнала нет) или символ 1 (сигнал есть).

Предполагается, что помеха в канале представляет собой гауссовский шум с нулевым средним и известной дисперсией, который взаимодействует с сигналом аддитивно (суммируется). Результатом обработки наблюдаемого колебания является случайная величина y, которая может иметь различное распределение в зависимости от того, есть ли сигнал в наблюдаемом колебании, а именно: распределение при гипотезе H₀ – «сигнала нет» – является гауссовским с нулевым средним, а распределение при гипотезе H₁ – «сигнал есть» – отличается сдвигом на величину a, зависящую от способа обработки (например, если обработка сводится к взятию отсчета в момент, когда несущее колебание достигает максимума, величина a представляет собой его амплитуду). Значение a предполагается известным.

Таким образом, проверяемые гипотезы описываются двумя условными плотностями распределения вероятностей w(y/H₀) и w(y/H₁), изображенными на рисунке 17.2.

Приемник в таком случае должен сравнить y с некоторым фиксированным значением (порогом) y_п и если y больше порога, принять решение о наличии сигнала, в противном случае – о его отсутствии, что можно кратко записать в следующей символической форме:

y ≥ y_п → «1»;

y ≤ y_п → «0».

Каким бы ни был порог y_п, очевидно, есть некоторая ненулевая вероятность p₀₁принять решение о наличии сигнала при его фактическом отсутствии. Эта вероятность называется условной вероятностью ошибки первого рода («ложная тревога») и определяется выражением:

.

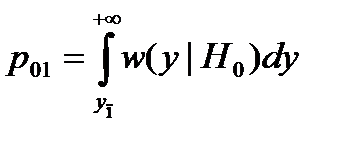Аналогично существует ненулевая вероятность принять решение об отсутствии сигнала, в то время как на самом деле он есть (условная вероятность ошибки второго рода, или пропуска сигнала):

.

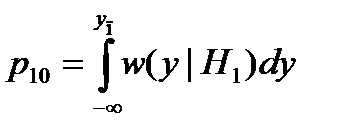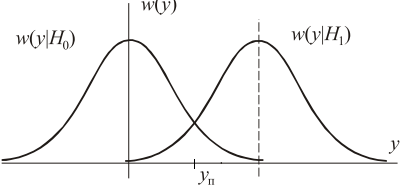
Рис. 17.2. Условные плотности распределения вероятностей величины y при простых гипотезах

Анализ рисунка 17.2 показывает, что сумма указанных условных вероятностей минимальна, если порог y_п находится как абсцисса точки пересечения условных плотностей w(y/H₀) и w(y/H₁).

Очевидно, при таком выборе порога приемник является оптимальным по критерию минимума суммарной условной вероятностиошибки(17.4) и принятие решения основывается на сравнении значений функций w(y/H₀) и w(y/H₁) при наблюдаемом значении y:

w(y|H₀ < w(y|H₁) → “1”

w(y|H₀ ≥ w(y|H₁) → “0”

Это правило принятия решения можно переписать также в форме:

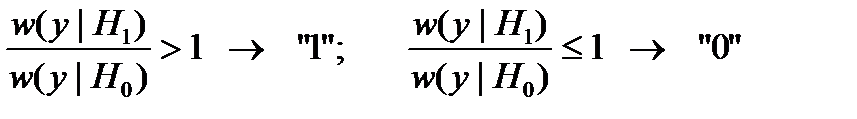. (17.5)

Решение, таким образом, принимается в пользу той гипотезы, которая представляется более правдоподобной при данном значении y, поэтому отношение 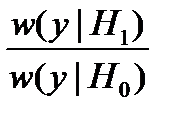называется отношением правдоподобияи обозначается Λ(y). Правило (17.5) называют правилом максимального правдоподобия. Заметим, что критерий (17.4) часто называют критерием максимума правдоподобия.

Критерий идеального наблюдателя предполагает учет априорных вероятностей гипотез. Оптимальный по этому критерию приемник обеспечивает минимум средней вероятности ошибки, т. е. наименьшую сумму безусловных вероятностей ошибок первого и второго рода. Иначе говоря, сравнению подлежат функции w(y/H₀) и w(y/H₁), умноженные на соответствующие априорные вероятности. Правило принятия решения в таком приемнике можно записать в форме:

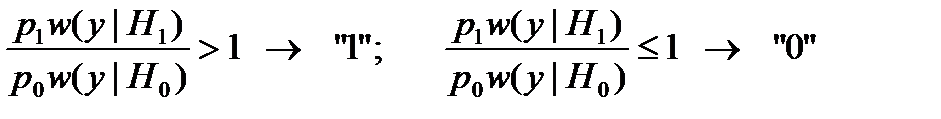
Используя понятие отношения правдоподобия, можно записать правило в виде:

,

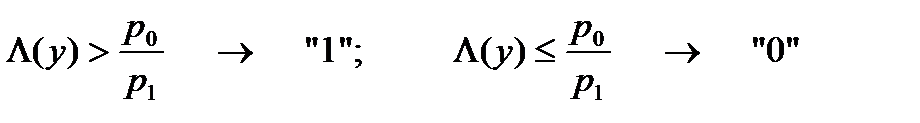при этом отношение правдоподобия сравнивается с пороговым значением, зависящим от априорных вероятностей.

Наконец, в случае байесовского критерия решение принимается по правилу:

,

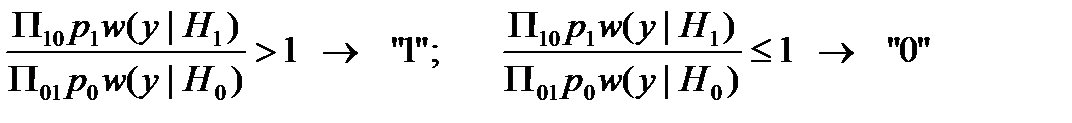или

.

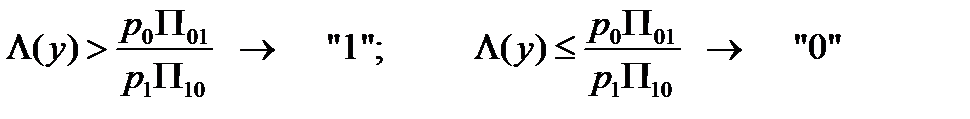Итак, во всех случаях оптимальный приемник «устроен одинаково»: для наблюдаемого значения y, зависящего от принятой реализации z(t), вычисляется значение отношения правдоподобия, которое сравнивается с порогом; порог равен 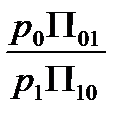для оптимального приемника по критерию минимума среднего риска, p₀ / p₁ для идеального приемника Котельникова и 1 для приемника максимального правдоподобия.

Следует отметим, что иногда удобнее вычислять не отношение правдоподобия, а его логарифм. В силу монотонности логарифмической функции это не влияет на условные вероятности ошибок, если порог также прологарифмировать.