Барометрическая формула. Закон распределения Больцмана.

При выводе основного уравнения молекулярно-кинетической теории газов предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Если газ находится в силовом поле, то существуют силы, которые сообщают хаотически движущимся молекулам направленное движение.

Молекулы газа, находящиеся в поле тяготения, участвуют в тепловом движении и испытывают действие силы тяжести. Тяготение и тепловое движение приводят к состоянию газа, при котором наблюдается убыль концентрации и давления газа с возрастанием высоты над землей.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова и равна m₀.

Атмосферное давление на некоторую площадку S обусловлено весом столба воздуха над этой площадкой (т.е. действием силы тяжести) (рис.6.8). Пусть на высоте h – давление р, а при h=0 – p=p₀. Рассмотрим изменение давления элемента “столба” высотой dh, в пределах которого концентрацию можно считать постоянной. Убыль давления в пределах dh:

.

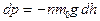(6.7.1)

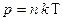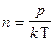Но , или , поэтому:

.

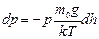(6.7.2)

Произведя разделение переменных: 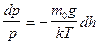, получим

.

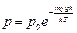(6.7.3)

Если учесть, что 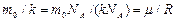, тогда

.

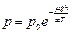(6.7.4)

Зависимость (6.7.4) давления атмосферы от высоты над уровнем моря при постоянной температуре называют барометрической формулой.

Пользуясь барометрической формулой 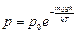, можно получить закон изменения концентрации с высотой. Приняв во внимание 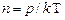и 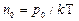, где n и n₀ – концентрация молекул на высоте h и h₀=0 и подставляя р и р₀ в барометрическую формулу, получим закон распределения концентраций по высоте:

,

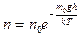(6.7.5)

Полученное распределение Больцмана справедливо для поля тяготения, для которого 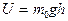– потенциальная энергия на высоте h (на разной высоте молекула обладает различным запасом потенциальной энергии). Однако оно справедливо и для идеального газа, находящегося в любом другом потенциальном поле:

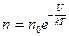
(6.7.6)

Данное выражение является распределением Больцмана в поле с потенциальной энергией U .

При Т® ¥, n®n₀, то есть происходит выравнивание концентрации газа по всему объему, занимаемому газом. При Т® 0, n® 0, то есть все молекулы опустятся на поверхность Земли (если речь идет об атмосфере).