Начальные понятия теории вероятностей

1. Опыт или испытание - совокупность условий, при которых данное событие может произойти.

Например, подсчёт простых предложений в тексте – это испытание, а обнаружение в тексте 56 простых предложений – это случайное событие.

Примеры испытаний: подбрасывание монеты или игральной кости, извлечение шара из урны с шарами, определение количества глаголов в фрагменте из стихов некоторого поэта и т.д.

2.Событие – исход испытания. События обозначаются большими латинскими буквами А, В, С, …

Событие может быть:

случайное– может произойти, а может и не произойти;

достоверное – произойдёт обязательно при данном испытании;

невозможное - никогда не произойдёт при данном испытании.

Примеры:

А=«появление буквы у после сочетания прыг» - случайное событие;

В=«появление буквы а или н или у после сочетания прыг» – достоверное событие; D=« появление буквы е после сочетания прыг» – невозможное событие; E=«в произвольно взятом отрывке текста данного автора длиной 100 словоформ содержится 12 глаголов» – случайное событие.

3. События называются несовместными, если наступление одного из них исключает появление любого другого. В противном случае события называются совместными.

Совместныесобытиямогут произойти вместе в одном испытании, несовместные – не могут произойти вместе.

Примеры:

А = «слово является глаголом» и В = «слово является сказуемым» при выборе из русского текста одного слова – совместные события;

К = «появилась буква д» и М= «появилась буква е» при выборе произвольно одной буквы русского алфавита – несовместные событие.

4.Равновозможные события –события, для которых нет оснований полагать, что одно из них более возможно, чем другое.

Примеры.

а) С=«на игральной кости выпало число 6» и D=«на игральной кости выпало число 1» – равновозможные события (исходя из предположения о симметричностиигрального кубика);

б) при произвольном выборе словоформы из определённого текста все возможные события считаются равновозможными, так как каждая словоформа имеет одинаковую возможность быть выбранной;

в) Е=« выбрана буква к» и F=«выбрана буква д» при произвольном выборе буквы из русского текста не являются равновозможными, так как частота употребления этих букв различна.

5.Полная группа событий – совокупность несовместных событий, которые могут произойти при данном испытании, т.е. обязательно произойдёт только одно из этих событий. Для одного испытания можно представить несколько полных групп, в зависимости от цели выбора

Пример. Из карточек с буквами слова ЛИК произвольно извлекают одну. Тогда полную группу могут составить события:

а) «выбрана буква Л»; «выбрана буква И»; «выбрана буква К»;

б) «выбрана гласная буква», «выбрана согласная буква».

6.Элементарными событиями (исходами) называются исходы некоторого испытания, если они образуют полную группу и являются равновозможными.Элементарное событие – нельзя представить в виде суммы двух или нескольких событий.

Пример. Произвольно выбирается буква русского алфавита. Событие D=«выбрана буква Я» – элементарное событие; событие F=«выбрана гласная буква» можно представить в виде суммы 11 событий, следовательно, F не является элементарным событием.

7. Противоположные события - несовместные события, такие, что если одно из них не произошло, то обязательно произойдёт другое. По определению, 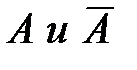образуют полную группу событий.

Пример. Из текста произвольно выбирают 3 слова. Событие А = «хотя бы одно из выбранных слов является местоимением», тогда

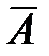= «ни одно из выбранных слов не является местоимением» -противоположное событие.

8. Событие А благоприятно событию В, если всегда, когда произойдёт А, произойдёт и В.

Пример. Событие «выбрана буква Я» благоприятно событию «выбрана гласная буква».

Лингвистическое испытание - это наблюдение (опыт или измерение) за поведением и признаками изучаемых лингвистических объектов. Результатом лингвистического испытания является лингвистическое событие.

Например, испытание состоит в угадывании буквы, стоящей после сочетания «которо..». События, которые могут произойти: А={появилась буква е}, В={ появилась буква г}, С={появилась буква м}, Д={ появилась буква й}. Все данные события являются случайными, элементарными, несовместными, и образуют полную группу. Достоверное событие - появление буквы «о» после сочетания «которог..». Появление любой другой буквы – невозможное событие. Событие А={появилась буква у} и событие 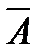={появился пробел} являются противоположными при угадывании буквы после цепочки «котором..» [Пиотровский, 1977, с.125].