Два сочетания отличаются только составом элементов.

Число сочетаний из n элементов по m обозначается 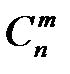и находится по формуле: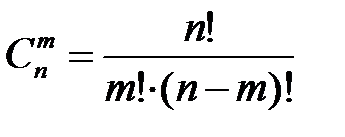

Пример. Из 10 гостей выбирают 2 для участия в конкурсе. Сколько имеется способов выбора?

При выборе 2 гостей не важен порядок их выбора, поэтому находим число сочетаний из 10 по 2: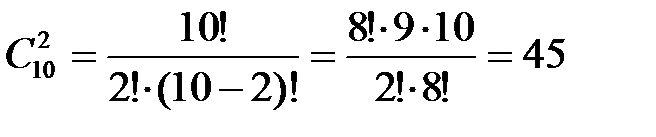

Число перестановок, размещений, сочетаний с повторениями (для тех случаев, когда среди образующих элементов есть одинаковые)

Число перестановок из n элементов с повторениями, где ni - количество одинаковых элементов в i – той группе: .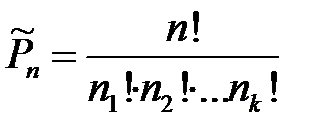

Пример. Найти количество комбинаций, которые можно составить из букв слова «математика».

Так как в слове «математика» буквы повторяются (м-2 раза, а-3 раза, т-2 раза), то полученные буквосочетания являются перестановками с повторением.

;

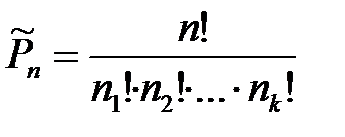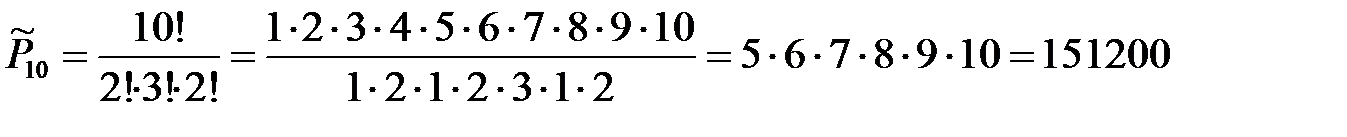
Число размещений из n элементов по m с повторениями: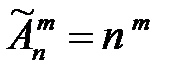

Пример. Сколько можно составить 2-буквенных комбинаций для денежных знаков из 30 букв русского алфавита ( без ъ, й, ь)?

Так как буквы в серии денежных знаков могут повторяться, то это размещения с повторениями: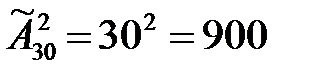

Число сочетаний из n элементов по m с повторениями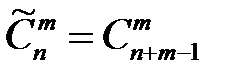

Пример. В некотором языке имеются 2 типа фонем: гласные и согласные, причём слово может быть образовано из одних гласных, из одних согласных, а также из гласных и согласных. Необходимо определить, сколькими способами можно составить 3-фонемное слово [22].

Так как выбираются 3 фонемы из 2 типов, причём типы фонем в слове могут повторяться, то число способов составления 3-фонемного слова

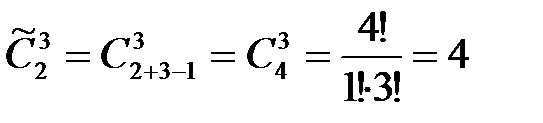
Эти способы можно перечислить: слово состоит из одних гласных, из одних согласных, из двух гласных и одной согласной и из одной гласной и двух согласных.

Основные понятия теории вероятностей

Явления или события, которые происходят вокруг нас, имеют разную возможность (или то же самое, вероятность) появления. На практике нам постоянно приходится оценивать эту возможность. Например, возможность выигрыша в лотерее, в которой из 1 миллиона билетов, только 100 выигрышных, мала и мы вряд ли примем в ней участие, но мы попытаем счастье в праздничном розыгрыше, где из100 билетов 50 выигрышных, так как вероятность выигрыша здесь гораздо больше. Однако мы не можем сказать, что в первом случае мы обязательно проиграем, а во втором – выиграем, т.е. событие «выигрыш» является случайным (может произойти, а может не произойти) и предсказать положительный результат невозможно. Но среди случайных явлений при большом количестве испытаний наблюдаются закономерности, которые и изучает теория вероятностей.

Теория вероятностей– раздел математики, изучающий закономерности, присущие массовым случайным явлениям.

Предметом теории вероятностей являются математические модели случайных явлений.

Цель – осуществление прогноза в области случайных явлений.

«Познавательная ценность теории вероятностей обусловлена тем, что массовые случайные явления в своём совокупном действии создают строгие закономерности. Само понятие математической вероятности было бы бесплодно, если не находило бы своего осуществления в виде частоты появления какого-либо результата при многократном повторении однородных условий». (Из предисловия А.Н. Колмогорова к сочинению Я. Бернулли «О законе больших чисел»).

Теория вероятностей возникла в середине XVII века. Её возникновение связано с исследованиями Б. Паскаля, П. Ферма, Х. Гюйгенса в области теории азартных игр. Примеры из этой области широко используют и в настоящее время, так как для них легко строить математические модели. Становление теории вероятностей как математической науки принадлежит швейцарскому математику Я. Бернулли, доказавшему для простейшего случая важнейшее положение теории вероятностей – закон больших чисел (1713г.). Дальнейшее развитие теории вероятностей связано с именами А. Муавра, П. Лапласа, К. Гаусса, С. Пуассона.

Большой вклад в развитие теории вероятностей внесли русские учёные В.Я. Буняковский, П.Л. Чебышев, А.М. Ляпунов, А.А. Марков, А.Я. Хинчин, А.Н. Колмогоров, Б.В. Гнеденко и другие.

В настоящее время методы теории вероятностей и математической статистики являются наиболее значимыми для лингвистических исследований, применяются в различных видах лингвистического анализа: стилистическом, диахроническом, типологическом, в социолингвистике, психолингвистике, лексикографии и других.