ІІ.5.5. Приложения теории фрактального расширения квадрата

Регулярность и комформность ре-зультатов различных итераций фрак- тального расширения квадрата явля-ются основой для практических при-ложений в различных отраслях народ-ного хозяйства. Эти приложения осно-ваны на материализации геометричес-ких идей этой теории.

1. Геометрия трещиноустойчивых

и самозамыкающихся структур дорожных покрытий.

Проблема качественных, долгове-чных и экономичных дорожных покры-тий актуальна в глобальных масштаб-бах. Причина этой актуальности кроет-

ся в низкой трещиноустойчивости спло-шного жесткого покрытия, так как про-цесс трещинообразования конструк-тивно неуправляем.

Если трещины в сплошнотелом по-крытии неизбежны, то такое покрытие следует заменить на сборное из таких комбинаторных элементов, швы между которыми были бы максимально изви-листыми и замкнутыми, ибо трещины, возвратившиеся к своему началу, гас-нут.

Рис. ІІ.46.Вариант дорожного покрытия из

29-клеточных фрактальных элементов

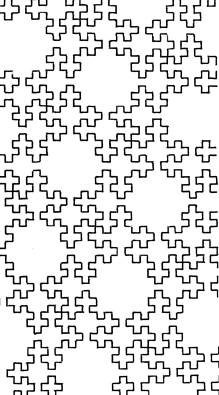
Рис. ІІ.47. Комбинаторное покрытие плоскости 169-клеточными элементами

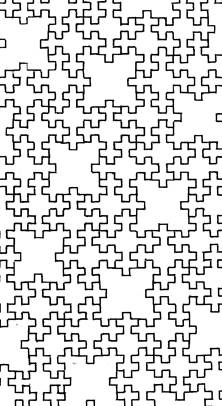
Рис. ІІ.48.Вариант дорожногопокрытия из 29-клеточных крестовых элементов и

53-клеточных вставок

Таким требованиям вполне удовлетворяет комбинаторное покрытие дороги из конгруэнт-ный 29-клеточных элементов, вступающих друг с другом в за-мковые соединения. (рис.ІІ.46.)Такая конструкция синергетич-на, так как обладает свойством самоорганизации, ибо напряже-ния в одних элементах, благо-даря связям между ними, пере-распределяются на всю сис-тему, которая, будучи сборной, работает как монолитная, но трещиноустойчивая.

Если рассмотреть комбина-торику 169-клеточных элемен-тов, то она представляется не-технологичной из-за слабости звена, соединяющего боковые элементы с центральным.(рис. ІІ.47). Этот недостаток легко ус-транить, перейдя на сборку из двух типоразмеров – 29-клеточ-ного элемента и вставок между ними, остающихся после их «сраста-ния» (см. рис. ІІ.37)

Комбинаторное покрытие плоскости 985-клеточными эле-ментами (рис.ІІ.50) содержит большую 445-клеточную сред-нюю часть, что технологически нерационально. Потому её мож-но упростить за счет структур-рирования фигуры наложения габаритных квадратов средних фигур на центральную (см.рис.ІІ.42) до 213-клеточного элемен-ра, который, в свою очередь, мо-жет состоять из центрального 29-клеточного креста и 4-х 41-клеточных угловых фигур с диа-гональной осью симметрии (рис.

ІІ.49).

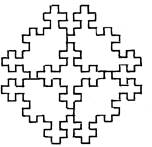
Рис. ІІ.49.Структурирование средней части центральной 213-клеточной фигуры, оставшейся после наложения бокових фигур на центральную

Рис. ІІ.50.Комбинаторикаиз985-клеточных фрактальных фигур

Рис. ІІ.51.Вариант мощения площади фрактальными элементов трёх типоразмеров

Приведенные варианты дорожного покрытия являються концептуальними и практически приемлемыми, но при ус-ловии индустриального производства фрактальных элементов из прочного и износоустойчивого материала, которые укладываются на прочное основание, которое также может быть синергети-ческим. В итоге структура покрытия по-лучается трещиноустойчивой и долго-вечной, простой в производстве работ, выполняемых в короткие сроки и с бо-льшим экономическим эффектом.

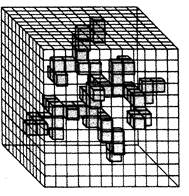
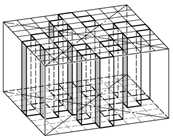
Рис. ІІ.52. Структурирование трёхмерно-го пространства и возможность материализации в нем абстрактных структур ( по Ж.Зейтуну)

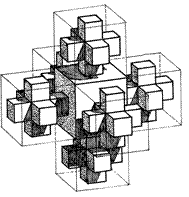
Рис. ІІ.53. Пространственный аналог второй итерации фрактального расширения квадрата

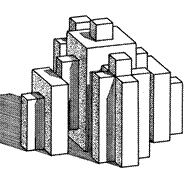
Рис. ІІ.54.Один из вариантовобъёмно-планировочного решения жилого дома на основе 29-клеточного результата фрактального расширения квадрата

2. Применение результатов фрактального расширения квадрата в архитектуре

Равносторонний прямоугольник или квадрат является наиболее про-стой единицей измерения площади лю-бой плоской фигуры. Если фигуру квад-рата представить как горизонтальную проекций куба, то последний явится на-иболее простой единицей измерения объёма того пространственного объек-та, который ортогонально проецируется в ту плоскую фигуру, площадь которой определяется числом расположенных в нем квадратов.

Регулярная сетка квадратов плотно упаковывает двумерную плоскость, а трёхмерный линейный каркас кубов плотно упаковывает трёхмерное прост-ранство [129] (рис.ІІ.52). Такая ситуа-ция позволяет проектировать трехмер-ные объекты путем материализации тех кубических элементов пространств-ва, структура которых предопределяет-ся их двумерной проекцией и рядом наложенный условий.

Если принять в качестве проектиру-емого объекта пространственный ана-лог 29-клеточного элемента фракталь-ного расширения квадрата (см.рис.ІІ.33) то в результате 5-клеточный крест пре-вратится в 7-кубовый пространствен-ный крест, центральный куб которого выростает из центрального квадрата 5-клеточного креста и содержит 27кубических ячеек, а в стру-ктуре остальных 6-ти 27-ячей-ковых габаритных кубов мате-риализуется только 7 кубичес-ких взаимосвязанных ячеек, образующих 6 конгруэнтных 7-ячейковых крестов, подобных 7-кубовому габаритному (рис.ІІ.53).

Из теории обратимых изо-бражений известно, что моно-проекция необратима, т.е., ме-жду элементами евклидова пространства и её плоскостью ортогональное проецирование устанавливает одно-многозна-чное соответствие. Это озна-чает что любой плоской ли-нейной конструкции в картине соответ-ствует однопараметрическое множеств-

во элементов в пространстве, элемен-

ты которых ортогонально проецируют-ся в соответствующие элементы этой конструкции. Отсюда вытекает чисто практический вывод: из великого мно-жества вариантов пространствен-ных интерпретаций какой-либо плос-кой горизонтальной плоской фигуры следует выбирать тот в качестве искомого, который наиболее оптима-льно удовлетворяет наложенным ус-ловиям.

Так, на основе фигуры 29-клеточно-го креста, принятого за план жилого дома, можно запроектировать его раз-личные варианты, объёмно-планиро-вочные решения которых будут удовле-творять любым наперед заданным ус-ловиям. Определившись с размерами модульного куба, центральный квадрат этажа следует отводить под лестнич-ные клетки и лифтовые площадки, а пятиклеточные кресты – под жилые по-мещения. Несущий каркас здания – сто-ечно-балочная регулярная система, ле-гко реализуемая в монолитном домо-строении.

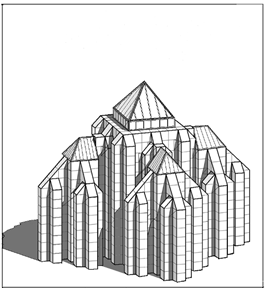
Если в качестве плана дома-комп-лекса принять фигуру 169-клеточного расширения квадрата, то в качестве её пространственных интерпретаций мо-жет быть принято большое количество различных объёмно-планировочных ре-шений, одно из которых приведено на рис.ІІ.55.

Рис. ІІ.55.Один извариантовфрактало-подобного террасного дома-комплекса с атриумом на основе 169-клеточного результата фрактального расширения квадрата

Рис. ІІ.56. Плёночный объёмный элемент для монтажа плоской

оболочки

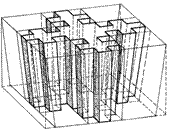
Рис. ІІ.57.Плёночный объёмный элемент для монтажа цилиндрической оболочки

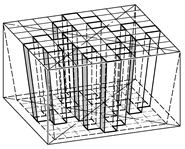
Рис. ІІ.58. Плёночный объёмный элемент для монтажа сферической оболочки

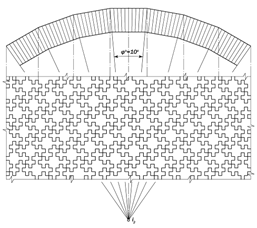
Рис. ІІ.59.Ортогональные проекции фрагмента цилиндрической фрактальной оболочки

Центральная часть этого комплекса формирует его атри-умное пространство с лифта-ми, лестницами и галереями, а пространства 4-х прилегаю-щих к нему крыльев могут быть использованы под торговые, жилые и офисные помещения.

Структурирование прост-ранства на основе 985-клеточ-ной снежинки Ткача-Нифанина даст ещё большее количество возможных объёмно-планиро-вочных решений вплоть, допу-стим, до подобия пирамиде фараона Хеопса.

3. Применение результатов фрактального расширения квадрата к проектированию пневмоконструкций.

Способность 29-клеточных крестовых фигур входить друг с другом в замковые соеди-нения привела к мысли о их изготов-лении из высокопрочной синтетичес-кой плёнки с внутренними перегород-ками для поддержания их формы. В полунадутом состоянии они легко вхо-дят в соединения, а после полного надувания придают всей сборной кон-струкции свойства монолитной. На этой основе можно говорить о принципиаль-ном конструировании пневматических оболочек различной формы и назначе-ния.

Если объемной интер-претацией этой фигуры будет 52-гранная призма, то такими элементами ст-руктурируется плоский слой пространства типа дорожного покрытия. Бу-дучи чрезвычайно лёгким, этот слой может стелить-ся по воде и служить быс-тровозводимым понтон-ным мостом или морским причалом. Естественно, что его параметры опре-деляются расчетом (рис. ІІ.56).

Если граням симмет-ричных одной из двух плоскостей сим-метрии половин 52-гранной призмы

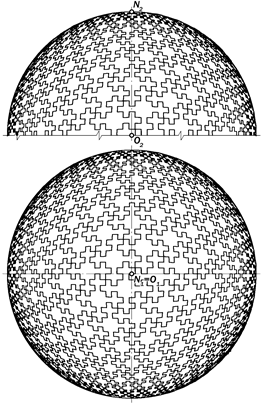
Рис. ІІ.60.Ортогональные проекции условной полусферической фрактальной оболочки

придать расчетный уклон, то из полу-ченных клинообразных объёмных эле-ментов можно смонтировать цилиндри-ческую круговую пневмооболочку (рис. ІІ.57, ІІ.59).Представляется, что в связи с лёгкостью элементов таких оболочек и прочностью связей между ними, они могут перекрывать большие площади и целые сооружения., служить больше- пролетными ангарами, складами и дру-гими объектами различного назначе-ния.

Если 52-гранную призму преобра-зовать в пирамиду, то из таких пирами-дальных элементов можно смонтиро-вать полусферическую пневмооболочку (рис. ІІ.58, ІІ.60), которая может служить как самостоятельным сооружением, так и четвертьсферическим завершением полуцилиндрической оболочки.

Достоинствами таких оболочек яв-ляются отсутствие необходимости под-держания избыточного давления вну-три сооружения, их большепролётность и долговечность. Выход из строя одно-го или нескольких элементов не влечёт разрушения конструкции, а лишь требу-ет их замены.Проблематична лишь кон-

струкция клапанов для подачи воздуха.