Правила комбинаторики

Лекция Комбинаторика.

Лингвисту часто приходится решать задачи, в которых требуется из конечного множества лингвистических элементов по заданным правилам составлять различные комбинации и производить подсчёт таких комбинаций. Например, «синтаксисту важно знать, сколько позиционных вариантов может давать в устно-разговорной речи предложение “Сегодня идёт дождь”, фонетисту - сколько, двух- и трёхбуквенных комбинаций может дать русский алфавит» (Пиотровский, 1977, с. 110). Задачи такого вида называются комбинаторными, а раздел математики, в котором решают такие задачи – комбинаторикой.

Комбинаторика – раздел математики, в котором изучаются вопросы о числе различных подмножеств (комбинаций), подчинённых тем или иным условиям, которые можно составить из элементов конечного множества.

Комбинаторика широко применяется на практике, в том числе и в языкознании. По словам В.М. Солнцева “способность к комбинаторике есть общее и обязательное свойство единиц языка, обусловленное общесистемными фундаментальными свойствами единиц языка – дискретностью и неоднородностью”(Солнцев, 1977, с. 268).

Комбинаторика связана с другими разделами математики, в том числе с теорией вероятностей, имеет широкий спектр применения в различных областях знаний.

Основоположником современной комбинаторики считается Г. Лейбниц, который ввёл термин «комбинаторика» в математический обиход в 1666 году, опубликовав свой труд «Рассуждения о комбинаторном искусстве». Наряду с Готфридом Лейбницем, большой вклад в развитии комбинаторики, как науки, внесли Блез Паскаль и Якоб Бернулли. Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера.

Правила комбинаторики

Многие задачи комбинаторики решаются с помощью двух основных правил: правила сложения и правила умножения.

Правило сложения.Пусть элемент А можно выбрать 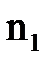способами, элемент В – другими 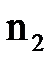способами. Тогда элемент А или В можно выбрать 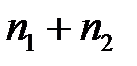способами.

Пример. На первой полке 10 книг, а на второй 12. Сколькими способами можно выбрать книгу с одной из этих полок?

Так как книгу с первой полки (элемент А) можно выбрать 10 способами, а книгу со второй (полки элемент В) – 12 способами, то книгу с первой или второй полки (элемент А или В) можно выбрать 10+12=22 способами.

Правило умножения.Пусть элемент А можно выбрать 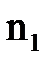способами, при каждом выборе А элемент В можно выбрать 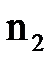способами,

Тогда элемент А и В можно выбрать 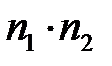способами.

Пример. Сколько слов можно получить, если для корня «изб» выбирается один из 3 суффиксов: «ушк», «ёнк», «ушечк», и одно из двух окончаний: «а», «и».

Есть 3 способа выбора суффикса и 2 способа выбора окончания, поэтому суффикс и окончание можно выбрать 3 2=6 способами, т.е. получится 6 слов.