Обратимые матрицы. Вычисление обратной матрицы
Определение 4.6.Матрица A ÎMnn(F)называется обратимой, если $ XÎ Mnn(F) A × X = X × A = En.
Матрица X называется обратной матрицей к А и обозначается A–1.
Определение 4.7.Квадратная матрица А ÎMnn(F) называется неособенной (невырожденной), если ее ранг равен порядку n этой матрицы.
Замечание.Квадратная матрица А ÎMnn(F) является неособенной (невырожденной) тогда и только тогда, когда |A| ¹ 0.
Теорема 4. 2 (критерий обратимости матрицы).Квадратная матрица АÎ Mnn(F) обратима тогда и только тогда, когдаона неособенная.
Теорема 4. 3 (о нахождении обратной матрицы).
1) Пусть А – неособенная матрица, А ÎMnn(F). Рассмотрим расширенную матрицу В = (A | Еn), которая получается из А приписыванием справа матрицы Еn. Если к матрице В применить элементарные преобразования строк так, чтобы слева от черты получилась матрица Еn, то справа от черты получится матрица А-1.
(A | Еn) ~ …~ … (Еn | A–1)
2) Пусть A Î Mnn(F). Если |A| ¹ 0, то A–1 = 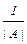 × || Aij|| t, где Aij – алгебраическое дополнение к элементу aij матрицы А (1 £ i £ n,1 £ j £ n).
× || Aij|| t, где Aij – алгебраическое дополнение к элементу aij матрицы А (1 £ i £ n,1 £ j £ n).
Пример.Вычислим обратную матрицу А-1 двумя способами:
А = 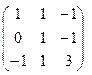 = rang A =3, значит, матрица A обратима.
= rang A =3, значит, матрица A обратима.
Вычислим А-1.
1. Метод элементарных преобразований: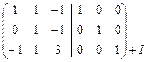 ~
~ 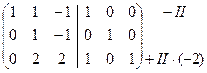 ~
~ 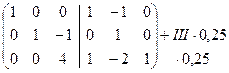 ~
~ 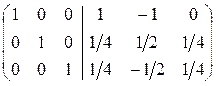 .Таким образом,
.Таким образом, 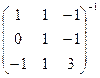 =
= 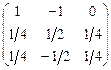 .
.
2. С помощью алгебраических дополнений:A–1 = 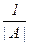 × || Aij || t (1 £ i £ n,1£ j £ n).
× || Aij || t (1 £ i £ n,1£ j £ n).
|A| = 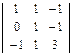 = (3 + 1 + 0) – (1 – 1 + 0) = 4
= (3 + 1 + 0) – (1 – 1 + 0) = 4 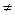 0. Поэтому А-1 обратима.
0. Поэтому А-1 обратима.
Вычисляем алгебраические дополнения элементов данной матрицы, не забывая о их знаках:
A11 = (-1)1+1· 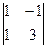 = 4, A12 = (-1)1+2 ·
= 4, A12 = (-1)1+2 · 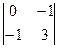 = 1, A13 = (-1)1+3 ·
= 1, A13 = (-1)1+3 · 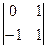 = 1,
= 1,
A21 = (-1)2+1 · 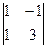 = – 4, A22 = (-1)2+2 ·
= – 4, A22 = (-1)2+2 · 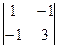 = 2, A23 = (-1)2+3 ·
= 2, A23 = (-1)2+3 · 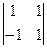 = –2,
= –2,
A31 = (-1)3+1 · 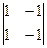 = 0, A32 = (-1)3+2 ·
= 0, A32 = (-1)3+2 · 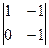 = 1, A33 = (-1)3+3 ·
= 1, A33 = (-1)3+3 · 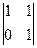 = 1.
= 1.
А-1 = 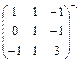 =
= 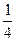 ×
× 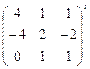 =
= 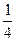 ×
× 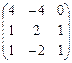 =
= 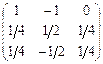 .
.
Проверка: А · А-1= 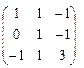 ·
· 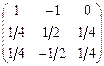 =
= 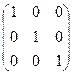 .
.
Ответ: А-1 = 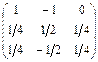 .
.
Дата добавления: 2021-12-14; просмотров: 530;











