Распределение Стьюдента (t-распределение).
В п.1 был рассмотрен закон распределения средней арифметической 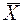 , зависящий от дисперсии
, зависящий от дисперсии 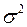 генеральной совокупности. Однако во многих практических приложениях значение параметра
генеральной совокупности. Однако во многих практических приложениях значение параметра 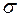 , как правило, неизвестно. Задачу определения закона распределения
, как правило, неизвестно. Задачу определения закона распределения 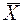 , не зависящего от
, не зависящего от 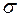 решил английский статистик В. Госсет (писавший под псевдонимом «Стьюдент») в 1908 году.
решил английский статистик В. Госсет (писавший под псевдонимом «Стьюдент») в 1908 году.
Дадим определение случайной величины, имеющей распределение Стьюдента:
Если случайная величина 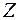 имеет нормированное нормальное распределение, а величина
имеет нормированное нормальное распределение, а величина 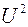 имеет распределение
имеет распределение 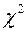 с
с 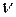 степенями свободы, причем
степенями свободы, причем 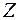 и
и 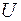 независимы, то случайная величина
независимы, то случайная величина
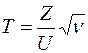
имеет t-распределение Стьюдента с числом степеней свободы равном 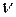 .
.
Функция плотности t-распределения задаётся формулой
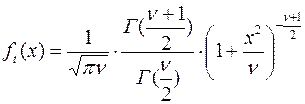 (4)
(4)
Из формулы (4) видно, что функция плотности чётная, следовательно, её график симметричен относительно оси ординат. При 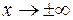 значение
значение 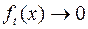 . Максимальное значение функция принимает в точке
. Максимальное значение функция принимает в точке 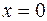 . Таким образом, вид графика функции (4) аналогичен графику функции плотности стандартного нормального распределения.
. Таким образом, вид графика функции (4) аналогичен графику функции плотности стандартного нормального распределения.
Построены таблицы критических точек t-распределения, в которых для заданного уровня 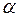 значимости для разных значений числа степеней свободы
значимости для разных значений числа степеней свободы 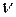 , приводятся числа, вероятность превышения которых равна уровню значимости
, приводятся числа, вероятность превышения которых равна уровню значимости 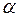 .
.
Распределение Стьюдента используется для построения интервальной оценки генеральной средней при неизвестном среднем квадратическом отклонении 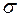 .
.
Дата добавления: 2021-12-14; просмотров: 501;











