Точечные оценки основных параметров распределений
Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какими выборочными характеристиками оцениваются эти параметры.
Будем рассматривать различные выборки случайной величины Х данного объёма n.
1. Средняя арифметическая
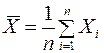
является несмещённой, состоятельной и эффективной оценкой математического ожидания (генеральной средней) 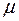 генеральной случайной величины Х с конечной дисперсией, в классе всех линейных оценок, т.е. оценок вида
генеральной случайной величины Х с конечной дисперсией, в классе всех линейных оценок, т.е. оценок вида
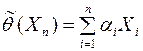 ,
,
где 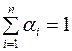 .
.
2. Выборочная дисперсия генеральной совокупности Х с конечной дисперсией 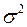
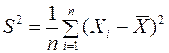
является смещённой состоятельной оценкой генеральной дисперсии 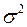 .
.
Несмещённой оценкой является исправленная выборочная дисперсия
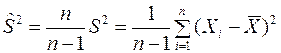 ,
,
где дробь 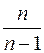 называется поправкой Бесселя. При малых значениях n эта дробь существенно отличается от единицы, с увеличением n она стремится к единице. При n>50 практически нет разницы между
называется поправкой Бесселя. При малых значениях n эта дробь существенно отличается от единицы, с увеличением n она стремится к единице. При n>50 практически нет разницы между 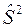 и
и 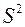 .
.
Замечание: Если известно значение математического ожидания 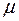 , то несмещённой, состоятельной и эффективной оценкой генеральной дисперсии является величина
, то несмещённой, состоятельной и эффективной оценкой генеральной дисперсии является величина
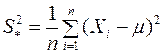
3. Если генеральная совокупность имеет биномиальное распределение, то несмещённой и состоятельной оценкой генеральной доли
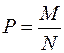 ,
,
где М – число наступлений некоторого события А, а N – объём генеральной совокупности, является выборочная доля
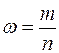 ,
,
где m – частота события А в выборке, а n – объем выборки.
Пусть по результатам n наблюдений построен вариационный дискретный ряд
| Варианты Xi | x1 | x2 | x3 | ..... | xm |
| Частоты ni | n1 | n2 | n3 | ..... | xm |
Тогда средняя арифметическая и выборочная дисперсия вычисляются по формулам:
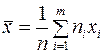
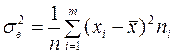
Отметим некоторые свойства этих величин:
1. Если все варианты увеличить в одно и тоже число k, то средняя арифметическая увеличится в k раз, а дисперсия в k2 раз.
2. Если все варианты изменить на одно и то же число c, то средняя арифметическая изменится на это же число, а дисперсия своего значения не изменит
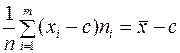 .
.
3. Если все частоты увеличить в одно и то же число раз, то средняя арифметическая и дисперсия не меняются.
Из этих свойств легко получить, так называемые, формулы упрощённого вычисления:
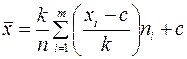 (1)
(1)
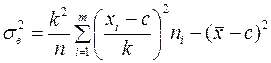 (2)
(2)
Пример 1. Дано распределение 1000 экземпляров северной сосны по диаметру ствола:
| Диаметр ствола (см) | Количество сосен | Диаметр ствола (см) | Количество сосен |
| 14-18 | 38-42 | ||
| 18-22 | 42-46 | ||
| 22-26 | 46-50 | ||
| 26-30 | 50-54 | ||
| 30-34 | 54-58 | ||
| 34-38 | Всего: |
Требуется вычислить среднюю арифметическую, выборочную дисперсию, среднее квадратическое отклонение.
Решение: Для вычисления применим формулы (1) и (2). Нам потребуется вариационный ряд данной выборки. В качестве вариант возьмём середины интервалов. Число с определим по наибольшей частоте. Все вычисления оформляются в таблице: c = 32, k = 4.
| Интервалы | Середины интервалов xi | Частоты ni | xi - c | 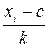
| 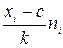
| 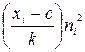
|
| 14-18 | -16 | -4 | -64 | |||
| 18-22 | -12 | -3 | -105 | |||
| 22-26 | -8 | -2 | -218 | |||
| 26-30 | -4 | -1 | -183 | |||
| 30-34 | ||||||
| 34-38 | ||||||
| 38-42 | ||||||
| 42-46 | ||||||
| 46-50 | ||||||
| 50-54 | ||||||
| 54-58 | ||||||
| Итого: | - | - | - |
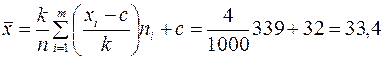
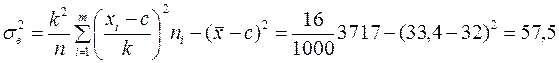
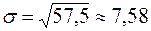 .
.
Замечание: для того, чтобы изучаемое свойство генеральной совокупности адекватно отражалось в выборке, она должна иметь случайный характер. Этого можно добиться разными способами. Приведём примеры некоторых из них:
1. Собственно-случайная выборка.
Суть метода можно описать следующей схемой: члены генеральной совокупности предварительно занумеровывают, и каждый номер записывают на отдельные карточки. Отбирая наудачу после тщательного перемешивания по одной карточке, получим выборку нужного объёма. Номера карточек укажут, какие члены генеральной совокупности попали в выборку. Возможны два принципиально различных подхода к образованию такой выборки в зависимости от того, возвращается отобранная карточка обратно после регистрации её номера или нет. В первом случае выборка называется повторной, во втором – бесповторной.
2. Механическая выборка.
Выборка называется механической, если члены генеральной совокупности отбираются через определенный интервал. Например, для 10% выборки отбирается каждый десятый член генеральной совокупности, для 20% - каждый пятый и т.п.
3. Типическая выборка.
Если члены генеральной совокупности предварительно разбить на группы по какому-нибудь признаку (например при изучении качества изделий целесообразно выделить изделия, производимые разными цехами, сменами, станками и т.д.), а в каждой группе произвести собственно-случайную выборку, то получим выборку, которую принято называть типической.
4. Серийная выборка.
Если указанные выше группы (серии) рассматривать, как элементы новой совокупности и из них образовывать собственно-случайную выборку, то полученная из членов выбранных серий совокупность называется серийной выборкой.
При составлении случайной выборки допускаются ошибки двух видов:
- Ошибка регистрации –так называется разница между истинным и наблюдавшимся значениями изучаемого признака. Эта ошибка может носить случайный или умышленный характер. Последнее недопустимо в исследованиях. В случае же случайной ошибки, рекомендуется провести повторную выборку.
- Ошибка репрезентативности – расхождение характеристик признака в генеральной и выборочной совокупности, связанного со случайным характером выборки. Такая ошибка всегда присутствует и задача математической статистики как раз и состоит в оценке величины этой ошибки.
Дата добавления: 2021-12-14; просмотров: 523;











