T-критерий Стьюдента или t-тест
t-критерий Стьюдента направлен на оценку различий величин средних Мх и Му двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у зависимых и независимых выборок, причем выборки могут быть не равны по величине.
1. Случай независимых выборок
Независимые выборки получаются при исследовании двух различных групп испытуемых (в нашем эксперименте это контрольная и опытная группы). В общем случае формула для расчета по t-критерию Стьюдента такова:
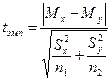 , (10.1)
, (10.1)
где Мх – средняя выборки Х;
Му – средняя выборки Y;
Sх – стандартное отклонение для выборки X;
sу – стандартное отклонение для выборки Y;
n1 и n2 – число элементов в первой и второй выборках.
Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда знаменатель выражения (10.1) примет вид:
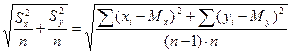 , (10.2)
, (10.2)
где 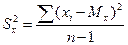 , а
, а 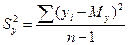 .
.
В случае неравночисленных выборок n1 ≠ n2, знаменатель выражения (10.1) будет вычисляться следующим образом:
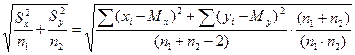 , (10.3)
, (10.3)
где 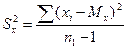 , а
, а 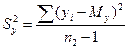 .
.
В обоих случаях подсчет числа степеней свободы осуществляется по формуле:
k = (п1 – 1) + (n2 – 1) = п1 + п2 – 2, (10.4)
где nl и n2, соответственно, величины первой и второй выборки.
Понятно, что при численном равенстве выборок k = 2∙n – 2 .
Теперь осталось лишь найти в таблице критических значений t (таблица 3 приложения 1) величину, соответствующую k степеням свободы, и сравнить эту величину с результатом расчета по формуле.
Если наш результат больше, чем значение для уровня достоверности 0,05 (вероятность 5%), найденное в таблице, то можно отбросить нулевую гипотезу (Но) и принять альтернативную гипотезу (Н1), т.е. считать разницу средних достоверной.
Если же, напротив, полученный при вычислении результат меньше, чем табличный (для k степеней свободы), то нулевую гипотезу нельзя отбросить, и, следовательно, разница средних недостоверна.
Рассмотрим пример использования t-критерия Стьюдента для независимых (несвязных) и неравных по численности выборок.
Задача 10.1. Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающиеся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.
Решение. Прежде всего, сформулируем гипотезы.
Н0: Средняя скорость сложной сенсомоторной реакции выбора в контрольной и экспериментальной группах не отличаются между собой.
Н1: Средняя скорость сложной сенсомоторной реакции выбора в контрольной и экспериментальной группах отличаются между собой.
Результаты эксперимента представим в виде таблицы 10.1, в которой произведем ряд необходимых расчетов.
Таблица 10.1
| № | Группы | Отклонения от среднего | Квадраты отклонений | |||
| X | Y | (хi-Mx) | (yi-My) | (хi-Mx)2 | (yi-My)2 | |
| - 22 | - 58 | |||||
| - 106 | ||||||
| - 17 | ||||||
| - 77 | ||||||
| - 36 | ||||||
| - 8 | ||||||
| – | - 56 | – | – | |||
| Сумма | ||||||
| Среднее |
Средние арифметические составляют в экспериментальной группе 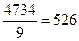 , в контрольной группе
, в контрольной группе 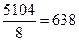 .
.
Разница по абсолютной величине между средними
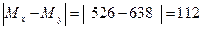 .
.
Подсчет выражения 10.3 дает:
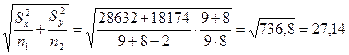 .
.
Тогда значение tэмп, вычисляемое по формуле (10.1), таково:
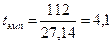 .
.
Число степеней свободы k = 9 + 8 – 2 =15.
По таблице 3 приложения 1 для данного числа степеней свободы находим:
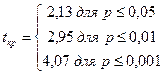
Строим «ось значимости».
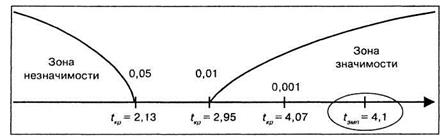
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,1% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом.
В терминах статистических гипотез это утверждение звучит так: гипотеза Н0 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза Н1 – о различии между экспериментальной и контрольными группами.
2. Случай зависимых выборок
К зависимым выборкам относятся, например, результаты одной и той же группы испытуемых до и после воздействия независимой переменной. В случае зависимых (связных) выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения tэмп осуществляется по формуле:
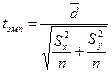 , (10.5)
, (10.5)
где 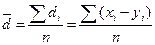 , (10.6)
, (10.6)
где di = xi – yi – разности между соответствующими значениями переменной X и переменной Y, а 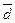 среднее этих разностей.
среднее этих разностей.
В свою очередь знаменатель выражения (10.5) вычисляется по следующей формуле:
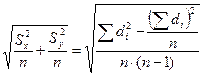 . (10.7)
. (10.7)
Полученные результаты сверяют с таблицей критических значений t (таблица 3 приложения 1), отыскивая в ней значения, соответствующие k = n – 1 степени свободы; n – это в данном случае число пар данных.
Перед тем как использовать формулу, необходимо вычислить для каждой группы частные разности между результатами во всех парах, квадрат каждой из этих разностей, сумму этих разностей и сумму их квадратов. Все эти расчеты необходимо сделать в чисто учебных целях. Сейчас существуют более быстрые методы, при которых основная работа сводится к вводу данных в программируемый микрокалькулятор или в компьютер, который автоматически выдает результат.
Рассмотрим пример использования t-критерия Стьюдента для зависимых (связных) и, очевидно, равных по численности выборок.
Задача 10.2. Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач.
Решение. Прежде всего, сформулируем гипотезы:
Н0: в результате научения время решения эквивалентных задач «игры в 5» не будет значимо изменяться.
Н1: в результате научения время решения эквивалентных задач «игры в 5» будет значимо изменяться.
Решение задачи представим в виде таблицы 10.2.
Таблица 10.2
| № испытуемого | 1 задача | 3 задача | d | d2 |
| 4,0 | 3,0 | 1,0 | 1,0 | |
| 3,5 | 3,0 | 0,5 | 0,25 | |
| 4,1 | 3,8 | 0,3 | 0,09 | |
| 5,5 | 2,1 | 3,4 | 11,56 | |
| 4,9 | -0,3 | 0,09 | ||
| 6,0 | 5,3 | 0,7 | 0,49 | |
| 5,1 | 3,1 | 2,0 | 4,00 | |
| 4,3 | 2,7 | 1,6 | 2,56 | |
| Суммы | 37,1 | 27,9 | 9,2 | 20,04 |
Вначале произведем расчет по формуле (10.6):
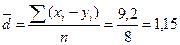 .
.
Затем применим формулу (10.7), получим:
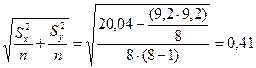 .
.
И, наконец, следует применить формулу (10.5). Получим:
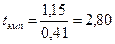 .
.
Число степеней свободы: k = 8 – 1 = 7 и по таблице 3 приложения 1 находим tкp:
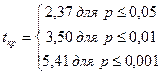
Строим «ось значимости».
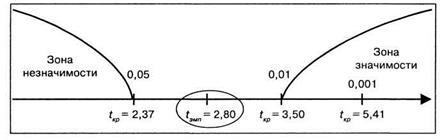
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее время решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Н0 отклоняется и принимается гипотеза Н1 – о различиях.
Для применения t-критерия Стьюдента необходимо соблюдать следующие условия:
1. Измерение может быть проведено в шкале интервалов и отношений.
2. Сравниваемые выборки должны быть распределены по нормальному закону.
F-критерий Фишера
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая в знаменателе. Формула вычисления по критерию Фишера F такова:
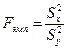 , (10.8)
, (10.8)
где 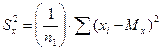 (10.9)
(10.9)
и 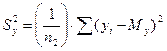 . (10.10)
. (10.10)
Поскольку, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице, т. е. Fэмп ≥ 1. Число степеней свободы определяется также просто: k1 = n1 – 1 для первой (т. е. для той выборки, величина дисперсии которой больше) и k2 = n2 – 1 для второй выборки. В таблице 4 приложения 1 критические значения критерия Фишера Fкр находятся по величинам k1 (верхняя строчка таблицы) и k2 (левый столбец таблицы).
Задача 10.3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос – есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах.
Сформулируем гипотезы.
Н0: различия в степени однородности показателей умственного развития между классами отсутствуют.
Н1: различия в степени однородности показателей умственного развития между классами присутствуют.
Результаты тестирования представлены в таблице 10.3.
Таблица 10.3
| № учащихся | Первый класс X | Второй класс Y | №№ учащихся n/n | Первый класс X | Второй класс Y |
| Суммы | |||||
| Среднее | 60,6 | 63,6 |
Как видно из таблицы, величины средних в обеих группах практически совпадают между собой 60,6 = 63,6 и величина t-критерия Стьюдента оказалась равной 0,347 и незначимой.
Рассчитав дисперсии для переменных X и Y, получаем
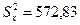 ;
; 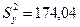 .
.
Тогда по формуле (10.8) для расчета по F критерию Фишера находим:
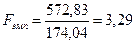 .
.
По таблице 4 приложения 1 для F критерия при степенях свободы в обоих случаях, равных k = 10 – 1 = 9, находим Fкp.
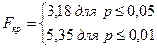
Строим «ось значимости».
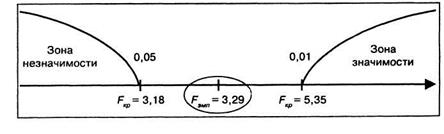
Таким образом, полученная величина Fэмп попала в зону неопределенности. В терминах статистических гипотез можно утверждать, что H0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н1. Психолог может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
Для применения критерия F Фишера необходимо соблюдать следующие условия:
1. Измерение может быть проведено в шкале интервалов и отношений.
2. Сравниваемые выборки должны быть распределены по нормальному закону.
Дата добавления: 2021-11-16; просмотров: 2264;











