Распределение средней арифметической.
Пусть над генеральной совокупностью, имеющей нормальный закон распределения 
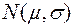 с математическим ожиданием
с математическим ожиданием 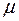 и средним квадратическим отклонением
и средним квадратическим отклонением 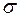 , проводится n независимых наблюдений X1, X2, …, Xn, образующих систему независимых одинаково распределённых случайных величин с распределением
, проводится n независимых наблюдений X1, X2, …, Xn, образующих систему независимых одинаково распределённых случайных величин с распределением 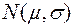 . Тогда средняя арифметическая
. Тогда средняя арифметическая
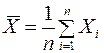
является случайной величиной и имеет нормальное распределение с параметрами 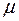 и
и 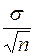 , т.е.
, т.е. 
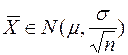 .
.
2. Распределение Пирсона ( 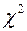 - хи квадрат).
- хи квадрат).
Если 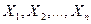 есть ряд независимых, нормированных, нормально распределённых случайных величин
есть ряд независимых, нормированных, нормально распределённых случайных величин 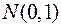 , то случайная величина
, то случайная величина
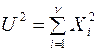 (3)
(3)
имеет распределение 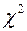 с
с 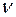 степенями свободы, где
степенями свободы, где 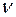 единственный параметр этого распределения, характеризующий число независимых случайных величин в выражении (3).
единственный параметр этого распределения, характеризующий число независимых случайных величин в выражении (3).
Плотность вероятностей распределения «хи квадрат» имеет вид:
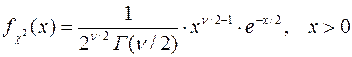 ,
,
где 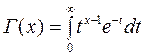 - гамма-функция Эйлера.
- гамма-функция Эйлера.
При 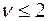 функция плотности убывает, а при
функция плотности убывает, а при 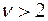 имеет единственный максимум в точке
имеет единственный максимум в точке 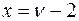 . График функции плотности изображён на рисунке.
. График функции плотности изображён на рисунке.

Основные числовые характеристики 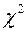 -распределения:
-распределения:
Математическое ожидание - 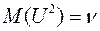 ;
;
Дисперсия - 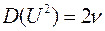 ;
;
Мода - 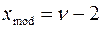 (существует только при
(существует только при 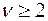 );
);
Распределение Пирсона используется для построения доверительного интервала для генеральной дисперсии.
Для этого распределения составлены таблиц критических значений, в которых для различных значений 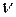 приводятся числа, вероятность превышения которых наблюдаемой случайной величиной равна заданному значению уровня значимости
приводятся числа, вероятность превышения которых наблюдаемой случайной величиной равна заданному значению уровня значимости 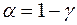 .
.
Дата добавления: 2021-12-14; просмотров: 490;











