Интервальные оценки для генеральной средней.

Правила построения доверительного интервала для математического ожидания зависят от того, известна или не известна дисперсия генеральной случайной величины.

1) Пусть из генеральной совокупности Х с нормальным законом распределения 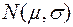и известной дисперсии 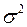взята случайная выборка объёмом n и вычислено средняя арифметическая 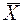. Требуется найти интервальную оценку математического ожидания генеральной случайной величины 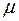. Поскольку 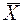имеет нормальное распределение с параметрами 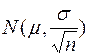, то статистика 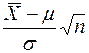имеет нормированное нормальное распределение с параметрами 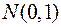. Тогда по интегральной теореме Лапласа имеем:

.

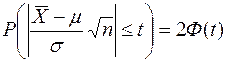Значение 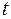при заданной доверительной вероятности найдём по таблице функции Лапласа из уравнения

.

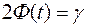Обозначим решение этого уравнения через 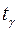, а искомый интервал найдём из неравенства

,

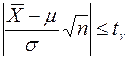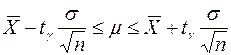(5)

Точность оценки равна

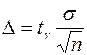(6)

Границы доверительного интервала равны:

Из формулы (6) можно при заданной точности 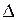найти необходимый объём выборки, а при заданном объёме и точности – доверительную вероятность.

2) Предположим теперь, что 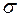в генеральной совокупности неизвестно, и вычислена выборочная дисперсия .

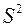В этом случае для построения интервальной оценки используется статистика

,

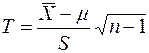имеющая распределение Стьюдента с числом степеней свободы .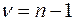

По таблице t-распределения для 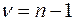степеней свободы, при заданном уровне значимости 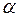, находим значение 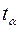, для которого справедливо равенство

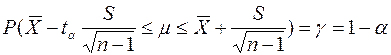, (7)

где точность оценки генеральной средней равна

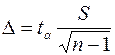(8)

При достаточно большём объёме выборки различие в доверительных интервалах (5) и (7) мало, так как при неограниченном увеличении числа n распределение Стьюдента стремится к нормальному распределению.

3) Приближённая интервальная оценка.

Пусть требуется найти интервальную оценку для математического ожидания в случае, когда закон распределения генеральной совокупности неизвестен. При достаточно большом объёме выборки средняя арифметическая, согласно центральной теореме Ляпунова, имеет распределение близкое к нормальному.

Поэтому доверительную вероятность можно вычислять по формуле:

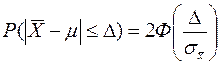(8)

где 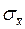- средняя квадратическая ошибка при замене 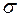на приближённое выборочное значение. В зависимости от цели образования выборки и способа отбора в неё элементов генеральной совокупности, получены следующие формулы средних квадратических ошибок:

Выборка	Повторная	Бесповторная
Цель выборки
Для средней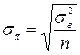

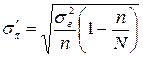
Здесь N- объём генеральной совокупности, n- объём выборки.

Минимальный объём выборки, гарантирующий попадание с надёжностью 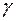параметра 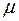в интервал 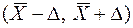при фиксированной предельной ошибке 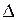, вычисляется по одной из формул:

Выборка	Повторная	Бесповторная
Цель выборки
Для средней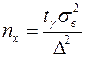

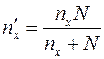
Здесь 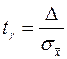находится с помощью таблицы из уравнения

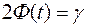. (9)

Рассмотрим решение некоторых типовых задач:

Задача 1. В условии примера 1. (Лекция 1.) найти:

1) Вероятность того, что среднее значение диаметра ствола сосен во всём массиве отличается от среднего диаметра в выборке не более чем на 0,5 см.

2) Границы, в которых с вероятностью 0,9544 заключён средний диаметр сосен всего массива.

3) Объём выборки, для которой доверительные границы с предельной ошибкой 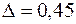см. имели бы место с доверительной вероятностью .

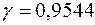Решение:

1) В примере 1 были подсчитаны выборочная средняя и дисперсия: .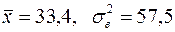

Подсчитаем среднюю квадратическую ошибку выборочной средней, учитывая, что объём генеральной совокупности (весь лесной массив) очень велик и формулы повторной и бесповторной выборок совпадают.

.

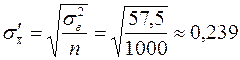Тогда из формулы (8) находим

.

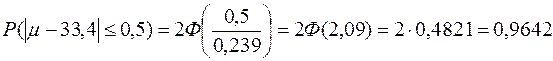2) По формуле (9) найдем такое значение t при котором

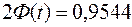
Из таблицы легко найти .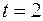

Тогда предельная ошибка выборки 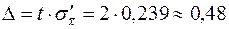. Доверительные границы будут равны:

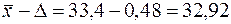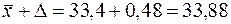(см.)

(см.)

3) Для ответа на третий вопрос задачи применим формулу объёма выборки как повторной при определении средней:

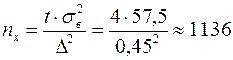(сосен)