Интервальные оценки для генеральной доли

Рассмотрим случай, когда объём выборки достаточно большёй (n > 30), а генеральная случайная величина распределена по биномиальному закону. Требуется оценить вероятность p наступления некоторого события А в каждом испытании по результатам n наблюдений.

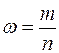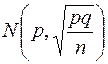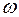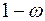При большом числе испытаний частость (выборочная доля) события А имеет приближённо нормальное распределение с параметрами , которые будем заменять выборочными значениями и для противоположного события 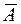. Тогда имеем:

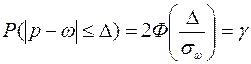(10)

Здесь 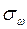- средняя квадратическая ошибка при оценке генеральной доли. Вычисляется в зависимости от способа образования выборки.

Выборка	Повторная	Бесповторная
Цель выборки
Для доли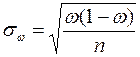

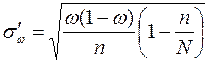
Для определения необходимого объёма выборки при фиксированной предельной ошибке 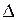, нетрудно получить формулы:

Выборка	Повторная	Бесповторная
Цель выборки
Для доли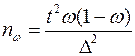

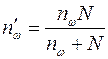
Задача 2. По данным примера 1. (лекция 1.) найти:

1) Доверительные границы, в которых с вероятностью 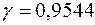находится во всём массиве доля сосен с диаметром ствола не меньше 46 см.

2) Каким должен быть объём выборки, чтобы с вероятностью 0,9544 гарантировать доверительные границы с предельной ошибкой ?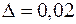

Решение:

1) Находим выборочную долю:

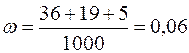
Подсчитаем среднюю квадратическую ошибку выборочной доли:

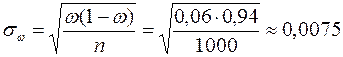
Значение t = 2 было найдено в задаче 1., тогда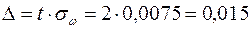

Доверительные границы равны:

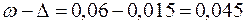
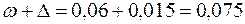
2) Необходимый объём выборки найдём по формуле:

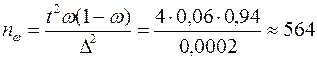(сосны)