Экспоненциальное распределение
Экспоненциальный закон адекватно описывает распределение длительности жизни 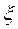 элемента, работающего в режиме нормальной эксплуатации, когда интенсивность отказа (коэффициент смертности) элемента в течение всего промежутка времени постоянна, равная
элемента, работающего в режиме нормальной эксплуатации, когда интенсивность отказа (коэффициент смертности) элемента в течение всего промежутка времени постоянна, равная 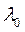 . Ниже приводятся функция распределения, плотность вероятностей и числовые характеристики этого закона:
. Ниже приводятся функция распределения, плотность вероятностей и числовые характеристики этого закона:
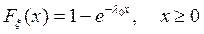 ;
;
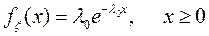 ;
;
среднее: 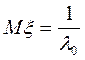 ;
;
мода: 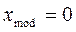 ;
;
медиана: 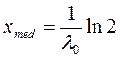 ;
;
дисперсия: 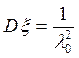 ;
;
Распределение, уравнение функции плотности которого имеет вид
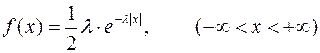 ,
,
называется двусторонним экспоненциальным распределением или распределением Лапласа. Числовые характеристики легко находятся:
среднее, мода и медиана равны 0;
дисперсия: 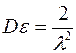 .
.
Симметричная, унимодальная функция плотности этого закона с острым максимумом в точке 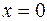 часто используется для описания распределения случайных ошибок
часто используется для описания распределения случайных ошибок 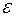 в моделях регрессионного типа.
в моделях регрессионного типа.
Ниже опишем три закона необходимых для построения разного рода статистических критериев и интервальных оценок параметров:
6. «Хи-квадрат»-распределение Пирсона с 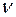 степенями свободы (
степенями свободы ( 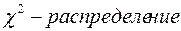 ).
).
Если 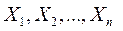 есть ряд независимых стандартно нормально распределённых случайных величин, т.е.
есть ряд независимых стандартно нормально распределённых случайных величин, т.е. 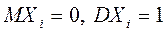 для
для 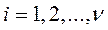 , то случайная величина
, то случайная величина
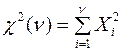 (2)
(2)
имеет распределение 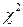 с
с 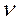 степенями свободы, где
степенями свободы, где 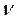 единственный параметр этого распределения, характеризующий число независимых случайных величин в выражении (2).
единственный параметр этого распределения, характеризующий число независимых случайных величин в выражении (2).
Такие суммы квадратов случайных величин впервые исследовал немецкий астроном Ф. Хельмерт в связи с применением гауссовской теории ошибок. Английский математик, статистик К. Пирсон построил функцию распределения, которую впоследствии стали называть функцией распределения «хи-квадрат». Для отрицательных 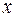 функция Пирсона
функция Пирсона 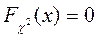 , а для неотрицательных
, а для неотрицательных 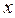
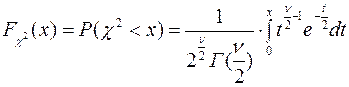 (3)
(3)
где Г(х) – интеграл Эйлера 2-ого рода или гамма-функция
Г(х) = 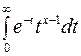 .
.
Соответствующая функция плотности вероятностей задаётся формулой:
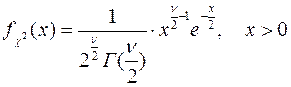 (4)
(4)
При 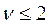 функция плотности постоянно убывает, а при
функция плотности постоянно убывает, а при 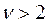 имеет единственный максимум в точке
имеет единственный максимум в точке 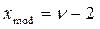 . График функции плотности при различных
. График функции плотности при различных 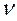 изображен на рисунке 9.1.
изображен на рисунке 9.1.
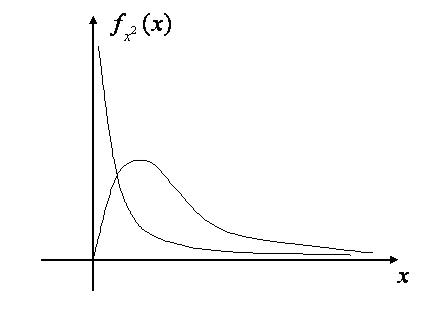
Рис. 9.1. график функции плотности распределения 
Основные числовые характеристики 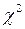 -распределения:
-распределения:
среднее: 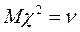 ;
;
мода: 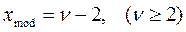 ;
;
дисперсия: 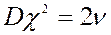 ;
;
асимметрия: 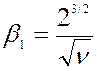 ;
;
эксцесс: 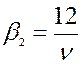 .
.
В таблицах для различных значений 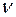 приводятся числа, вероятность превышения которых случайной величиной
приводятся числа, вероятность превышения которых случайной величиной 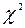 равна заданному значению уровня значимости
равна заданному значению уровня значимости 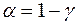 .
.
Распределение Пирсона используется для построения доверительного интервала для генеральной дисперсии.
7. Распределение Стьюдента с 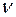 степенями свободы
степенями свободы
(t-распределение)
В нормальном распределении средняя арифметическая зависит от дисперсии слагаемых величин. Однако на практике дисперсия исследуемой величины, как правило, неизвестна. В этой связи возникла задача определения закона распределения 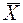 , не зависящего от
, не зависящего от 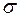 , которую решил английский статистик В. Госсет, публиковавшийся под псевдонимом Стьюдент. Дадим следующее определение:
, которую решил английский статистик В. Госсет, публиковавшийся под псевдонимом Стьюдент. Дадим следующее определение:
Если случайная величина Z имеет нормальное нормированное распределение N(0,1), а величина U2 имеет распределение 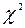 с
с 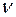 степенями свободы, причем Z и U взаимно независимы, то случайная величина
степенями свободы, причем Z и U взаимно независимы, то случайная величина
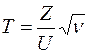
имеет t-распределение с 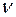 степенями свободы. Плотность распределения описывается формулой
степенями свободы. Плотность распределения описывается формулой
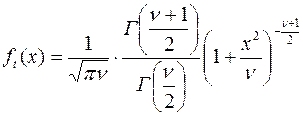 .
.
Функция плотности является унимодальной и симметричной относительно 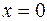 . Основные числовые характеристики:
. Основные числовые характеристики:
среднее, мода, медиана: 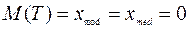 ;
;
дисперсия: 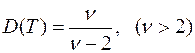 ;
;
асимметрия: 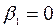 ;
;
эксцесс: 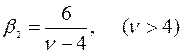 .
.
Ниже на рисунке приведены сравнительные графики функции плотности t-распределения при 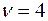 и стандартного нормального распределения N(0,1).
и стандартного нормального распределения N(0,1).
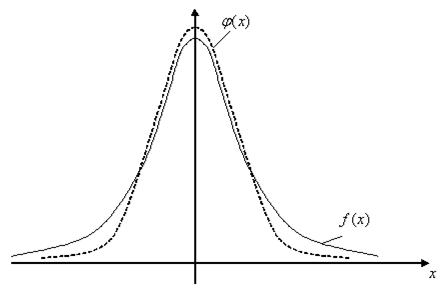
Рис. 9.2.График t-распределения при 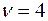
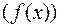 и нормального нормированного распределения
и нормального нормированного распределения 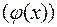
Если из генеральной совокупности Х с нормальным законом распределения 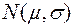 взята случайная выборка объёма n, то статистика
взята случайная выборка объёма n, то статистика
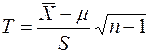
имеет распределение Стьюдента с 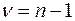 степенями свободы. Здесь S-выборочное среднее квадратическое отклонение.
степенями свободы. Здесь S-выборочное среднее квадратическое отклонение.
Распределение Стьюдента используется при интервальной оценке математического ожидания при неизвестном значении среднего квадратического отклонения 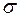 .
.
Дата добавления: 2021-12-14; просмотров: 568;











