Биномиальное распределение
Пусть имеется последовательность независимых испытаний удовлетворяющих схеме Бернулли: в результате каждого испытания некоторое интересующее событие А может произойти или нет. Причем при многократном (n-кратном) повторении эксперимента вероятность p осуществления события А остаётся одной и той же. Можно описать такую последовательность в терминах случайных величин, сопоставляя с i-м экспериментом данной последовательности случайную величину
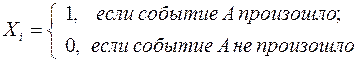
Тогда 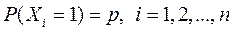 , причем случайные величины
, причем случайные величины 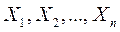 являются независимыми. Биномиальный закон описывает распределение случайной величины
являются независимыми. Биномиальный закон описывает распределение случайной величины
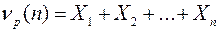 ,
,
т.е. числа появлений интересующего нас события в последовательности из n независимых испытаний, когда вероятность появления этого события в одном испытании равна p.
Очевидно, что 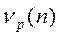 принимает только неотрицательные целые значения с вероятностями
принимает только неотрицательные целые значения с вероятностями
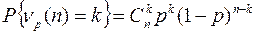
Основные числовые характеристики биномиального закона:
среднее: 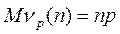 ;
;
мода хмод: 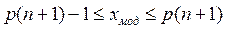 ;
;
дисперсия: 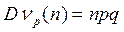 ;
;
асимметрия: 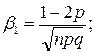
эксцесс: 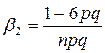 .
.
Дата добавления: 2021-12-14; просмотров: 502;











