Неравенство Чебышева

Вероятность того, что отклонение случайной величины Х от своего математического ожидания M(X) = a по абсолютной величине, будет больше произвольного положительного числа 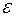, не превосходит дроби, в числителе которой стоит дисперсия, в знаменателе число .

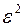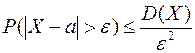(11)

Доказательство: Используя лемму Маркова и определение дисперсии легко понять следующее неравенство:

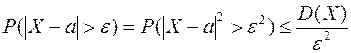
Для вероятности противоположного неравенства имеем неравенство:

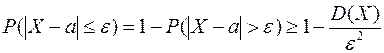(12)

В частности, если X – частота наступления некоторого события, то для частости этого события справедливо неравенство:

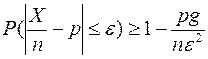(13)

Примеры:

1) Всхожесть семян некоторого растения 70%. Оценить вероятность того, что при посеве 10 000 семян отклонение доли взошедших от вероятности, что взойдет каждое из них, не больше чем 0,01.

Решение: Событие, состоящее в том, что посеянное семечко взойдет, обозначим через А. Число наступлений события А является случайной величиной Х. Математическое ожидание частости события А равно его вероятности и определяет всхожесть посева

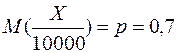
Согласно неравенству (13), искомая вероятность оценивается следующим образом:

.

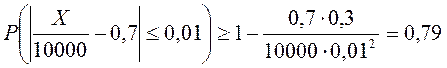2) В некоторых технологических условиях вероятность изготовления детали с дефектом равна 0,1. Оценить вероятность того, что из 10 000 изготовленных деталей с дефектом окажутся от 950 до 1030. Можно ли применить неравенство Чебышева? Как надо изменить правую границу, чтобы применение неравенства Чебышева стало возможным? Решить задачу.

Решение: Неравенство Чебышева оценивает неравенство с модулем, которое равносильно двойному неравенству, выражающего собой промежуток симметричный относительно математического ожидания случайной величины 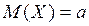. Границы этого промежутка равны .

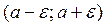В нашем случае математическое ожидание числа деталей Х, изготовленных с дефектом, равно 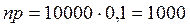. Таким образом, левая граница отстоит на 50, а правая на 30 единиц. Для симметричности необходимо правую границу изменить на 50. Тогда, учитывая, что дисперсия 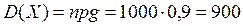, а число 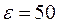, из формулы (11) находим:

.

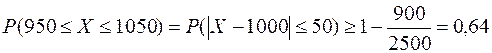Теорема Чебышева

Пусть 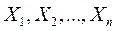- последовательность независимых случайных величин, имеющих дисперсии, ограниченные в совокупности некоторым числом C. Тогда средняя арифметическая этих случайных величин сходится по вероятности к средней арифметической их математических ожиданий, т.е.

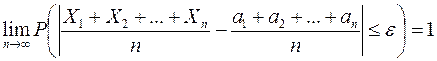(14)

Доказательство: Для независимых случайных величин справедливо равенство

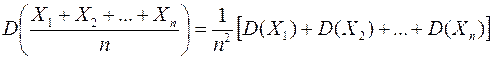
Учитывая, что для всех 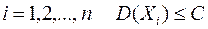, получим

(*)

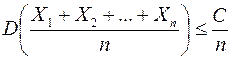Из неравенства Чебышева (11) и, с учетом оценки (*), вытекает следующее неравенство

.

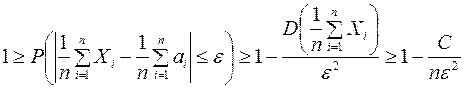Таким образом, при любом фиксированном значении числа 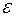, с увеличением числа n вероятность стремится к единице.

Смысл полученных результатов заключается в том, что при осреднении большого числа случайных величин все менее ощущается характерный для случайных величин неконтролируемый разброс значений, так что в пределе при 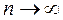этот разброс исчезает вовсе, или, как принято говорить, случайная величина вырождается в неслучайную. Однако при любом конечном числе слагаемых случайный разброс у среднего арифметического остается. Поэтому возникает вопрос исследования характера этого разброса. Фундаментальный результат в этом направлении известен как «центральная предельная теорема» был впервые сформулирован Лапласом и заключается в том, что для широкого класса независимых случайных величин предельный закон распределения их нормированной суммы вне зависимости от типа распределения слагаемых стремится к нормальному закону распределения.

Приведем конкретную формулировку, уточняющую сказанное выше предложение.