Интегральная предельная теорема Лапласа
Пусть событие А в каждом из n независимых испытаний наступает с постоянной вероятностью р. Тогда вероятность того, что при достаточно большом числе испытаний событие А наступит от m1 до m2 раз вычисляется по формуле:
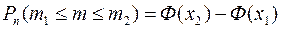 , (8)
, (8)
где 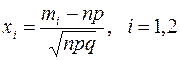
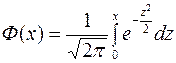 (9)
(9)
Функцию Ф(х) называют интегральной функцией Лапласа. Её значения табулированы. Рассмотрим некоторые свойства интегральной функции Лапласа.
Свойства функции Ф(х):
1) Ф(х) – нечетная функция, т.е. Ф(-х) = -Ф(х).
2) Ф(х) имеет две горизонтальные асимптоты y = 0,5 и y = -0,5.
Действительно, 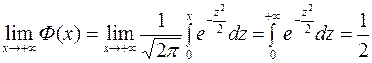
В последнем равенстве использовался так называемый интеграл Пуассона:
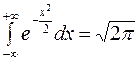
Ввиду нечетности функции Лапласа
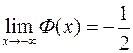
Причем приближение к числу 0,5 настолько быстрое, что для практических целей достаточно при 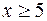 считать значение Ф(х) = 0,5.
считать значение Ф(х) = 0,5.
3) Из свойства интеграла с переменным верхним пределом от непрерывной функции следует равенство
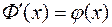
Пример: Вероятность поражения мишени стрелком равна 0,75. Определить вероятность того, что при 100 выстрелах он поразит мишень:
а) не менее 71, но не более 80 раз;
б) не менее 81 раза.
Решение: Обозначим p = 0,75, n = 100, m – число попаданий в мишень. Тогда
a) 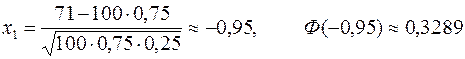
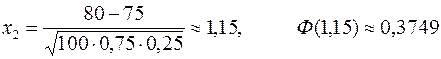
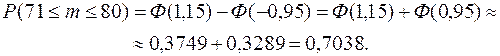
б) 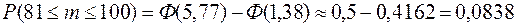
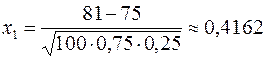
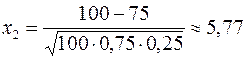
В статистике вероятность р наступления события А заменяют его частостью 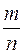 , причем чем больше n, тем меньше значение частости отклоняется от значения вероятности. Однако сколь тесной окажется эта близость предугадать невозможно. Тем не менее, имеет место следующая теорема.
, причем чем больше n, тем меньше значение частости отклоняется от значения вероятности. Однако сколь тесной окажется эта близость предугадать невозможно. Тем не менее, имеет место следующая теорема.
Теорема Бернулли: Для любого положительного числа 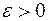 справедливо равенство
справедливо равенство
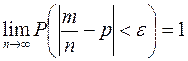 (10)
(10)
Доказательство: 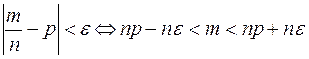 ,
,
тогда
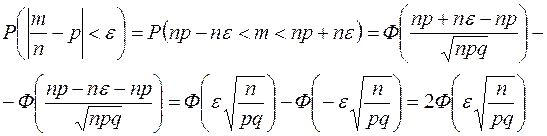
Учитывая свойство (2) функции Ф(х) и переходя к пределу при 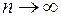 , получим равенство (10). Теорема Бернулли представляет собой одну из первых формулировок Закона больших чисел.
, получим равенство (10). Теорема Бернулли представляет собой одну из первых формулировок Закона больших чисел.
Замечания: Итак, мы рассмотрели различные случаи изменения величин n, m, p. Каждому из них соответствовала своя предельная теорема. При этом надо руководствоваться следующим:
1) Формулы Бернулли, Лапласа и Пуассона применяются в тех случаях, когда испытания удовлетворяют схеме Бернулли, т.е.
а) проводимые испытания независимы;
б) каждое испытание имеет только два исхода, либо наступает событие А, либо противоположное ему событие;
в) вероятность появления события А в каждом испытании постоянна и равна р.
2) Если число испытаний не велико, то для вычисления вероятности 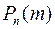 применяют формулу Бернулли.
применяют формулу Бернулли.
3) Если n мало и требуется найти вероятность появления события А от m1 до m2 раз, то применяют формулу
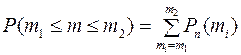 (11)
(11)
4) Если n достаточно велико, и вероятность наступления события А также не маленькая то 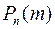 вычисляется по формуле Лапласа (6).
вычисляется по формуле Лапласа (6).
5) Если n велико, а р – мало, то используют асимптотическую формулу Пуассона (7).
6) Если число испытаний n достаточно велико, то
а) при малом числе слагаемых в сумме (11) и 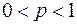 применяют формулу
применяют формулу
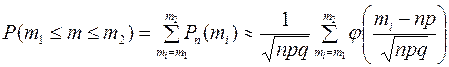 (12)
(12)
б) при малом числе слагаемых и малом р
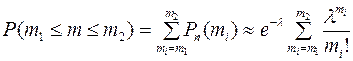 (13)
(13)
в) при большом числе слагаемых в сумме
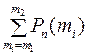
применяют интегральную формулу Лапласа (8).
Лекция 6. Дискретная случайная величина
и ее числовые характеристики
Виды случайных величин. Способы описания дискретной
случайной величины
Случайной называют величину, которая в результате испытания принимает одно и только одно из возможных своих значений, которое наперед неизвестно и зависит от причин, которые заранее не могут быть учтены.
Обозначают случайные величины прописными латинскими буквами последней части алфавита, например X, Y, Z, и т.д. Значения случайной величины обозначают строчными буквами. Например, 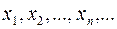 - значения случайной величины Х.
- значения случайной величины Х.
Различают два вида случайных величин: дискретные и непрерывные.
Дискретной называется случайная величина, принимающая отдельные изолированные значения.
Например: число мальчиков, родившихся из 100 детей, является дискретной случайной величиной, принимающей значения 0, 1, 2, …, 100.
Непрерывной называется случайная величина, которая может принимать всевозможные значения из некоторого конечного или бесконечного промежутка.
Например: На отрезок наудачу бросается точка. Абсцисса этой точки является непрерывной случайной величиной.
Всякую случайную величину задают с помощью закона распределения.
Законом распределения дискретной случайной величины называют перечень всех её возможных значений и вероятностей, с которыми они принимаются.
Этот закон задаётся таблицей
| Х | х1 | х2 | … | xn | … |
| Р | p1 | p2 | … | pn | … |
Так как в результате испытания случайная величина принимает только одно возможное значение, то очевидно, что события, состоящие в том, что случайная величина Х примет значения 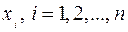 образуют полную группу и сумма их вероятностей равна 1, т.е.
образуют полную группу и сумма их вероятностей равна 1, т.е.
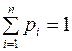
Если число значений бесконечно, то ряд, составленный из вероятностей указанных событий, сходится к 1.
Пример 1. В денежной лотерее 1000 билетов. Разыгрываются:
1 выигрыш в 1000 рублей,
4 выигрыша по 500 рублей,
5 выигрышей по400 рублей,
10 выигрышей по 100 рублей.
Составить закон распределения стоимости выигрыша для владельца одного лотерейного билета.
Решение: Стоимость возможного выигрыша является дискретной случайной величиной Х. Её возможные значения – 1000, 500, 400, 100, 0. Соответствующие вероятности равны – 0,001, 0,004, 0,005, 0,01, 0,98. Таблица распределения имеет вид
| Х | |||||
| Р | 0,001 | 0,004 | 0,005 | 0,01 | 0,98 |
Пример 2. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первым стрелком равна 0,5, вторым – 0,4.
Составить закон распределения числа попаданий в мишень обоими стрелками.
Решение: Обозначим через Х случайную величину – число попаданий в мишень обоими стрелками. Её возможные значения равны – 0, 1, 2. Обозначим через А1 событие, состоящее в том, что первый стрелок поразит цель. Событие А2 – второй стрелок поразит цель. Очевидно, эти события независимы. Тогда
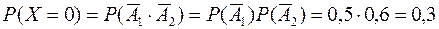
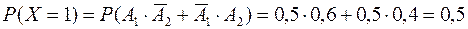
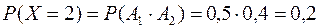 .
.
Таблица распределения имеет вид
| Х | |||
| Р | 0,3 | 0,5 | 0,2 |
Пример 3. Вероятность попадания стрелка в цель при одном выстреле равна р = 0,6. Составить закон распределения числа попаданий в цель, если стрелок производит 4 выстрела по цели.
Решение: Пусть Х – число попаданий в цель при 4 выстрелах. Поскольку каждый выстрел имеет два исхода – попал или не попал, причем попадание в цель имеет постоянную вероятность – 0,6, а сами исходы независимы, то вероятности значений с.в. Х вычисляются по формуле Бернулли
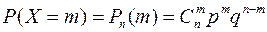 .
.
Тогда
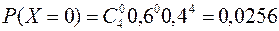
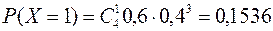
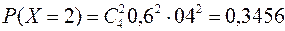
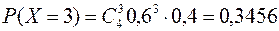
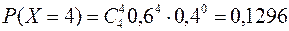
| X | |||||
| P | 0,0256 | 0,1536 | 0,3456 | 0,3456 | 0,1296 |
Пример 4. Студент ищет нужную ему книгу. Вероятность того, что он найдет эту книгу в библиотеке, равна 0,3. В городе 4 библиотеки. Составьте закон распределения числа посещенных библиотек.
Решение: Пусть Х- число посещенных библиотек. Так как посещение каждой следующей библиотеки зависит от результата посещения предыдущей, то применение формулы Бернулли не возможно.
Очевидно, что с.в. Х принимает значения 1, 2, 3, 4. Одну библиотеку он посетит, если в ней есть нужная ему книга. Вероятность этого исхода равна 0,3. Две библиотеки посетит, если в первой книгу не нашел, а во второй нашел. Тогда вероятность этого события равна 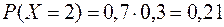 . Студент посетит три библиотеки, если не найдет книгу в первых двух. Вероятность этого события равна
. Студент посетит три библиотеки, если не найдет книгу в первых двух. Вероятность этого события равна 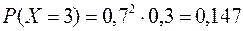 . И, наконец, он посетит все 4 библиотеки, если не найдет нужной книги в трех предыдущих библиотеках. Вероятность этого события равна
. И, наконец, он посетит все 4 библиотеки, если не найдет нужной книги в трех предыдущих библиотеках. Вероятность этого события равна 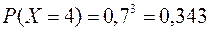 . Таблица распределения имеет вид:
. Таблица распределения имеет вид:
| Х | ||||
| Р | 0,3 | 0,21 | 0,147 | 0,343 |
Замечание: при решении задачи часто допускается одна ошибка, характерная для задач подобного типа. Вероятность посещения четырех библиотек вычисляется в предположении, что в трех предыдущих книга не найдена, но в четвертой она есть. При этом совсем не учитывается возможность отсутствия книги и в четвертой библиотеке. Ошибка легко находится при сложении всех вероятностей – их сумма не будет равна 1.
В некоторых задачах неправильные рассуждения приводят к комичным ситуациям. Рассмотрим традиционную задачу об охотнике.
Пример 5. Охотник стреляет по дичи, но успевает сделать не более четырёх выстрелов. Составить закон распределения числа промахов, если вероятность попадания при каждом выстреле равна 0,7.
Решение: Пусть Х – число промахов. Очевидно с.в. Х принимает значения 0, 1, 2, 3, 4. Причем 0 промахов означает, что охотник попал в дичь с первого выстрела. Тогда
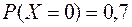
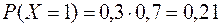
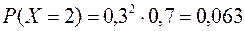
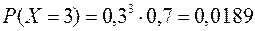
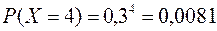
Таблица распределения имеет вид:
| Х | |||||
| Р | 0,7 | 0,21 | 0,063 | 0,0189 | 0,0081 |
При анализе задачи на вопрос «Что означает 0 промахов?», многие отвечают, что охотник 4 раза попал. И только через некоторое время до некоторых начинает доходить абсурдность этого утверждения.
Мы подробно рассмотрели способ задания дискретной случайной величины через закон распределения. Непрерывную случайную величину задать таким способом просто невозможно. Мало того, вероятность принятия конкретного значения непрерывной случайной величиной всегда равна нулю. Следовательно, непрерывную случайную величину надо задавать не отдельными вероятностями, вероятностью того, что она примет значения из некоторого промежутка.
Поэтому был предложен другой, более универсальный способ описания случайной величины через функцию её распределения.
Дата добавления: 2021-12-14; просмотров: 802;











