Локальная предельная теорема Муавра-Лапласа

При большом числе испытаний применение формулы Бернулли становится нецелесообразным в связи с громоздкостью вычислений. В таких случаях предпочтительнее применение предельных формул при неограниченном увеличении числа n.

Теорема: Если вероятность появления события А в каждом испытании постоянна и равна p, причем p не мало, то вероятность того, что событие А в n независимых испытаниях наступит ровно m раз, когда число испытаний неограниченно возрастает, приближенно вычисляют по формуле:

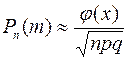(6)

Где 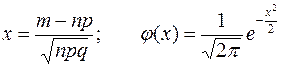- функция Лапласа или функция плотности вероятностей нормированного нормального распределения. Значения этой функции табулированы. Для того, чтобы пользоваться таблицей, необходимо знать следующие свойства функции Лапласа:

1) Функция 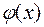- четная, т.е. 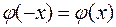для всех .

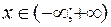По этой причине в таблице указаны значения функции лишь для положительных аргументов.

2) 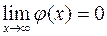, причем убывание значений функции настолько быстрое что при 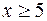считают .

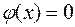Замечание: Точность формулы (6) существенно зависит от величин n и p. Анализ показывает, что точность улучшается с ростом произведения npq. Обычно формулу Лапласа используют при 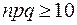. Отсюда видно, что чем ближе одно из чисел p или q к нулю, тем больше должно быть число испытаний n. Пусть p мало. Нас интересует оценка вероятности появления события А в n независимых испытаниях некоторого числа раз для большого числа n. Примерами таких событий могут служить: рождение близнецов, авария на городском транспорте, достижение столетнего возраста и т.п. Искомую оценку дает предельная теорема Пуассона.

Теорема: Пусть число m появления события А фиксировано, а числа n и p меняются, а именно 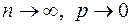так, что величина 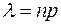остается ограниченной. Тогда справедлива асимптотическая формула:

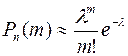(7)

Доказательство: Подставим в формулу Бернулли 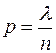, тогда

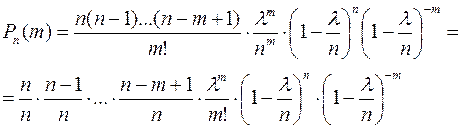
Очевидно 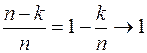, при фиксированном значении k и .

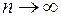Выражение 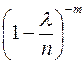так же стремится к 1 при 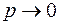и постоянном значении m. Используя второй замечательный предел, найдем:

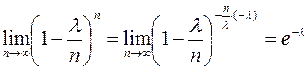
Из этих вычислений следует асимптотическая формула Пуассона:

.

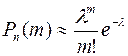Отметим, что в некоторых учебниках так же имеются таблицы значении вероятностей, определяемых формулой (7).

При решении практических задач гораздо чаще требуется определять вероятность появления события А в некотором промежутке. Такую задачу решает интегральная теорема Лапласа.