Лекция 5. Независимые испытания. Формула Бернулли.
Пусть имеется некоторое пространство элементарных событий U.
Под испытанием будем, как и прежде, понимать осуществление некоторого комплекса условий, в результате которого может произойти одно из событий пространства U.
Математической моделью последовательности n испытаний является новое пространство Un элементарных событий, состоящее из точек (e1, e2, …,en), где ei – произвольная точка пространства U, отвечающая испытанию с номером i.
Например, если U = {E1, E2, …, E6}, где Еi – число очков на выпавшей грани игральной кости при одном подбрасывании. Тогда пространство U3, соответствующее трем испытаниям, состоит из 63 = 216 точек (е1, е2, е3). Здесь е1 - это одно из событий пространства U и принимает 6 значений. Тоже самое для е2 и е3.
Пусть при s-том испытании пространство U подразделяется на k попарно несовместных случайных событий, т.е.

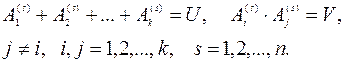
Событие 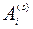 - назовем i-ым исходом при s-том испытании.
- назовем i-ым исходом при s-том испытании.
Обозначим 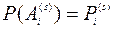 , тогда
, тогда 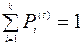 . Рассмотрим сложное событие
. Рассмотрим сложное событие 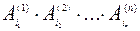 .
.
n – последовательных испытаний назовем независимыми, если
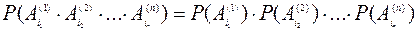
для любых 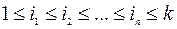 .
.
Теорема 1. Если данные n испытаний независимы, то любые m из них так же независимы.
Теорема 2. Для того чтобы n последовательных испытаний были независимы, необходимо и достаточно, чтобы выполнялось условие:
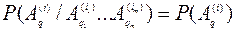
для любых чисел 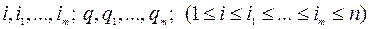 ,
,
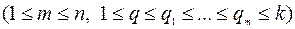
В дальнейшем мы ограничимся случаем, когда вероятности событий 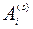 не зависят от номера испытания s. Обозначим в этом случае
не зависят от номера испытания s. Обозначим в этом случае 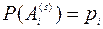 ,
, 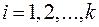 .
.
В силу несовместности единственной возможности исходов 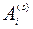 имеем:
имеем: 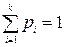 . Эта схема была впервые рассмотрена Я. Бернулли при k = 2. У него:
. Эта схема была впервые рассмотрена Я. Бернулли при k = 2. У него:
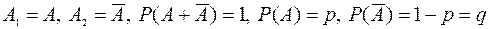
Формула Бернулли
Итак, будем рассматривать независимые испытания, в каждом из которых имеется только два исхода: либо наступает событие А, либо противоположное событие 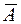 . Причем наступление события А происходит каждый раз с одинаковой вероятностью p.
. Причем наступление события А происходит каждый раз с одинаковой вероятностью p.
Применительно к этой схеме независимых испытаний, ставится задача определения вероятности 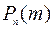 того, что при n независимых испытаниях событие А наступит m раз, а остальные n-m раз наступит событие
того, что при n независимых испытаниях событие А наступит m раз, а остальные n-m раз наступит событие 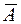 . Описанный результат испытаний обозначим через
. Описанный результат испытаний обозначим через 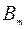 . Тогда это событие можно представить в виде суммы:
. Тогда это событие можно представить в виде суммы:
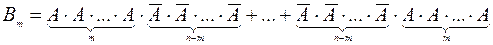
Слагаемые попарно несовместны и их число равно 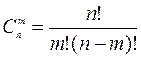 .
.
Вероятность каждого слагаемого равна 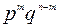 . Тогда вероятность события Bm вычисляется по формуле Бернулли:
. Тогда вероятность события Bm вычисляется по формуле Бернулли:
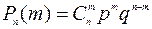 (1)
(1)
Рассмотрим обобщение формулы Бернулли. Пусть в каждом испытании может появиться одно из k несовместных событий Ai, и пусть P(Ai) = pi. Поставим следующую задачу: Найти вероятность того, что событие А1 появится m1 раз, событие А2 – m2 раза, и т.д., событие Аk – mk раз. При  чем m1+m2+…+mk = n. Тогда искомая вероятность равна
чем m1+m2+…+mk = n. Тогда искомая вероятность равна
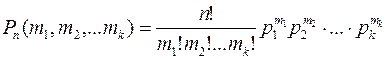 (2)
(2)
Примеры:
1) Статистикой установлено, что из тысячи родившихся детей в среднем рождается 485 девочек и 515 мальчиков. Найти вероятность того, что из пяти родившихся детей будет:
a) 3 девочки, б) не боле 3-х девочек, в) не менее двух и не более четырех девочек.
Решение: обозначим через А событие, состоящее в рождении девочки, а через m число родившихся девочек. Тогда:
а) 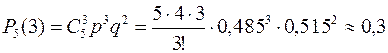
б) 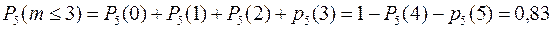
в) 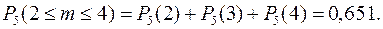
2)Проводится 10 бросаний игральной кости. Какова вероятность того, что один раз выпадет два очка, два раза три очка, четыре раза пять очков и три раза шесть очков?
Решение: Событие Аi – выпадение i очков при одном бросании игральной кости, i = 1,2, …, 6, mi – число появления события Ai в 10 испытаниях. Тогда искомая вероятность вычисляется по формуле (2)
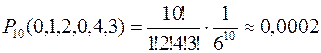
Дата добавления: 2021-12-14; просмотров: 753;











