Математическое ожидание и дисперсия дискретной случайной величины
Пусть дискретная случайная величина имеет распределение
| Х | х1 | х2 | … | xn |
| Р | p1 | p2 | … | pn |
Математическим ожиданием называют число равное сумме произведений значений случайной величины на соответствующие вероятности. Обозначают
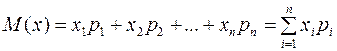
Если случайная величина принимает счетное множество значений, то математическое ожидание есть сумма ряда
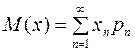 .
.
Прежде чем рассматривать свойства математического ожидания, определим операции над случайными величинами.
1. Произведением случайной величины Х на число k назовем новую случайную величину kX, значения которой равны значениям исходной случайной величины Х умноженные на число k и принимаются с теми же вероятностями.
2. Квадратом случайной величины Х называют новую случайную величину Х2, значения которой равны квадратам значений случайной величины Х и принимаются с теми же вероятностями.
При этом надо иметь в виду, что в результате возведения в квадрат некоторые значения становятся одинаковыми. В этом случае новое значение записывают один раз, а соответствующие вероятности складывают.
| X2 | |||
| P | 0,25 | 0,5 | 0,25 |
| X | -2 | |||
| P | 0,15 | 0,25 | 0,35 | 0,25 |
3. Суммой двух случайных величин Х и Y называют новую случайную величину, значения которой равны всевозможным значениям величин Х и Y, а соответствующие вероятности перемножаются, если X и Y независимы. В случае зависимости случайных величин вероятность значения X умножается на условную вероятность значения Y. При этом так же новые значения могут повторяться. Их записывают один раз, а вероятности повторяющихся значений складывают.
Рассмотрим задачу: Два баскетболиста по очереди забрасывают мяч в корзину. Всего сделано пять бросков. Вероятность попадания при одном броске первым баскетболистом равна 0,8, вторым – 0,9.
Составить таблицу распределения числа попаданий в корзину обоими баскетболистами.
Решение: Обозначим число попаданий первым баскетболистом через Х, вторым – Y. Первый игрок, согласно условию задачи, сделает три броска, второй – 2. Поскольку результаты бросков не зависят друг от друга, то мы находимся в условиях схемы Бернулли, и вероятности значений случайных величин Х и Y будем подсчитывать по формуле Бернулли
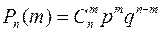
После не сложных вычислений, получим следующие распределения случайных величин Х и Y:
| Х | |||
| P | 0,01 | 0,18 | 0,81 |
| Х | ||||
| P | 0,008 | 0,096 | 0,384 | 0,512 |
Для построения суммы, составим таблицу:
| X | Y | X+Y | Pij | X | Y | X+Y | Pij | |
| 0,00008 | 0,00384 | |||||||
| 0,00144 | 0,06912 | |||||||
| 0,00648 | 0,31104 | |||||||
| 0,00096 | 0,00512 | |||||||
| 0,01728 | 0,09216 | |||||||
| 0,07776 | 0,41472 |
Составим теперь новую таблицу распределения суммы, записывая каждое значение по одному разу. Вероятности повторяющихся значений будем складывать:
| X+Y | ||||||
| P | 0,00008 | 0,0024 | 0,0276 | 0,152 | 0,4032 | 0,41472 |
4. Произведением двух независимых случайных величин называется новая случайная величина, значения которой равны всевозможным значениям случайных величин X и Y, при этом соответствующие вероятности перемножаются.
Дата добавления: 2021-12-14; просмотров: 581;











