Свойства функции распределения
1. Функция распределения принимает значения на промежутке [0,1]
2. Функция F(x) – неубывающая функция:
Пусть 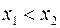 . Рассмотрим следующие события
. Рассмотрим следующие события
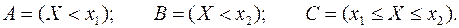
Тогда 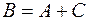 и
и 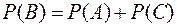 . Учитывая, что
. Учитывая, что
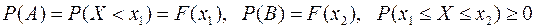 ,
,
получим 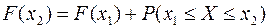 , что и доказывает неравенство:
, что и доказывает неравенство: 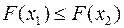 .
.
3. Справедливо равенство: 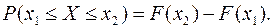
4. 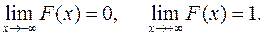
5. Функция распределения имеет не более счетного множества точек разрыва, причем только «скачков».
6. В каждой точке разрыва функция распределения непрерывна слева.
Замечание: каждая функция распределения удовлетворяет перечисленным свойствам. Верно и обратное, если функция удовлетворяет указанным свойствам, то она может рассматриваться как функция распределения некоторой случайной величины.
При этом надо иметь ввиду, что если случайная величина однозначно определяет свою функцию распределения, то существует сколь угодно случайных величин имеющих данную функцию распределения. Например, если случайная величина Х принимает два значения 1 или -1 с вероятностями 0,5, то случайная величина Y = -X, также принимает значения -1 и 1 с вероятностями 0,5. Однако, ясно, что Y всегда отлична от Х. Не трудно проверить, обе случайные величины имеют одну и туже функцию распределения
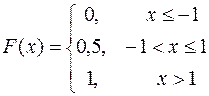
Из определения дискретной случайной величины следует, что её функция распределения имеет вид
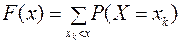 .
.
Дата добавления: 2021-12-14; просмотров: 594;











