Независимые события. Теорема умножения
Определение 2. Событие А независимо от события В, если его условная вероятность совпадает с безусловной, т.е.
P(A/B) = P(A)
Теорема 1. Если событие А независимо от события В, то и событие В не зависит от события А.
Действительно: 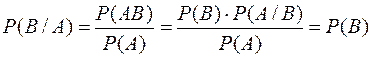 .
.
Пример 3. В урне лежат3 белых и 5 черных шаров. Последовательно извлекают два шара. Сравним два события:
А – извлеченный шар во втором испытании – белый,
В – извлеченный шар в первом испытании – белый,
если
а) первый шар возвращают обратно в урну перед вторым испытанием,
б) первый шар не возвращают обратно в урну.
Тогда в случае
а) 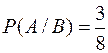 ;
; 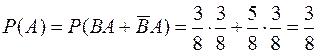 ;
;
Таким образом, P(A/B) = P(A), следовательно, события независимы.
б) 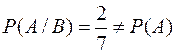 , следовательно события А и В зависимы.
, следовательно события А и В зависимы.
Теорема 3. Если события А и В независимы, то независимы и каждые два события 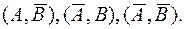
Определение 3. События А1, А2, …, Аn называются попарно независимыми, если независимы всякие два из них, т.е.
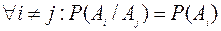
Определение 4. События А1, А2, …, Аn называются независимыми в совокупности или просто независимыми, если независимы каждое из них и любое произведение остальных, т.е.
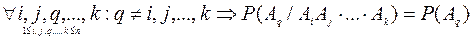
Замечание: Из независимости в совокупности следует попарная независимость событий. Обратное утверждение неверно. Приведем пример Бернштейна:
Пусть грани тетраэдра окрашены в разные цвета: первая грань в красный цвет, вторая в зеленый, третья в синий, четвертая во все три цвета. Производится подбрасывание тетраэдра, который может упасть на одну из граней. Обозначим через события А, В, С падение тетраэдра, соответственно, на красны, зеленый или синий цвета.
Покажем, что события А, В, С попарно независимы, но не являются независимыми в совокупности.
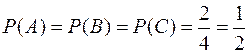 ,
,
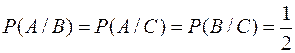 ,
,
Таким образом, события попарно не зависимы. Однако
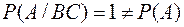 .
.
Без доказательства сформулируем следующие теоремы.
Теорема 4. Если события А1, А2, …, Аn независимы в совокупности, то какова бы ни была группа 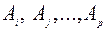 , составленная из этих событий, вероятность наступления всех событий этой группы равна произведению вероятностей каждого из них, т.е.
, составленная из этих событий, вероятность наступления всех событий этой группы равна произведению вероятностей каждого из них, т.е.
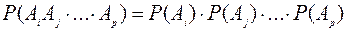 .
.
Имеет место и обратная теорема.
Теорема 5. События А1, А2, …, Аn независимы в совокупности, если для любой группы событий 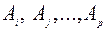
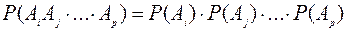 .
.
Пример 4. Вероятность попадания в цель из первого орудия равна 0,9, из второго – 0,8, из третьего – 0,7. Найти вероятность того, что при одновременном залпе из трех орудий, будет иметь место:
1). Одно поражение цели.
2). Хотя бы одно поражение цели.
Решение: Обозначим через событие Аi – поражение цели i-м орудием, i = 1,2,3. Тогда
1) Событие А – одно поражение цели.
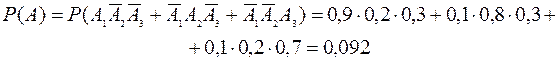
2) Событие А – хотя бы одно поражение цели.
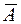 - ни одного попадания в цель. Тогда
- ни одного попадания в цель. Тогда
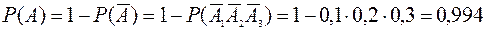
Теорема 6. Вероятность наступления хотя бы одного из n независимых событий равна разности между единицей и произведением вероятностей противоположных событий.
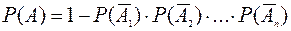
Следствие: Если вероятность наступления каждого события одинакова, т.е. P(Ai) = p, 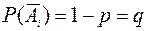 , то
, то
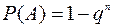 .
.
Дата добавления: 2021-12-14; просмотров: 594;











