Лекция 4. Условная вероятность. Теорема умножения. Независимые события. Формула полной вероятности
Определение 1. Вероятность события А, вычисленную в предположении, что событие В наступило, называют условной вероятностью и обозначают PB(A) или P(A/B).
Проследим за различием безусловной и условной вероятности на примере.
Пример 1. Из колоды в 36 карт последовательно вынимают две карты. Найти:
1) безусловную вероятность того, что вторая карта окажется тузом;
2) условную вероятность, что вторая карта окажется тузом, если первая карта была туз.
Решение: Обозначим через событие А – появление туза на втором месте, а через событие В – появление туза на первом месте. Тогда
1) событие А можно представить в виде следующей суммы несовместных событий:
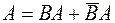 ,
,
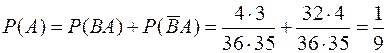 .
.
2) Если предположить, что первая вытащенная карта – туз, т.е. событие В наступило, то условная вероятность равна
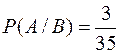 .
.
Рассмотрим решение задачи отыскания условной вероятности в общем виде для классического определения: Пусть из полной группы попарно несовместных и равновозможных событий А1, А2, … , Аn, событию А благоприятствуют m исходов, событию В – k исходов и событию АВ – r исходов данной группы событий.
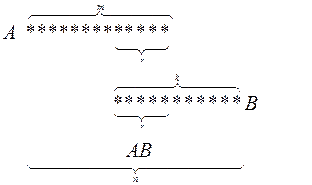
Если событие В произошло, то это означает, что наступило одно из k событий Aj, благоприятствующих событию В. При этом условии событию А благоприятствуют r и только r событий Aj, благоприятствующих событию АВ. Тогда
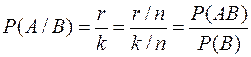 .
.
Аналогично доказывается, что
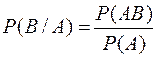 .
.
Из полученных формул находим, что
P(AB) = P(B)P(A/B) = P(A)P(B/A) (1)
Таким образом доказана теорема умножения:
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие наступило.
Следствие: Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, при условии, что все предыдущие события наступили.
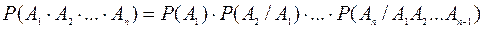 (2)
(2)
Пример 2.В урне лежат 5 белых, 4 черных и 3 синих шаров. Каждое испытание состоит в том, что извлекается наудачу один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный, при третьем – синий.
Решение: Обозначим вероятности появления шаров в последовательных испытаниях через Б, Ч, С. Тогда
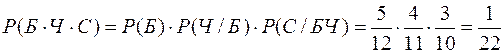
Условная вероятность обладает всеми свойствами вероятностей, так как она удовлетворяет системе аксиом 1-3.
Действительно:
1) Для любого А определена неотрицательная функция
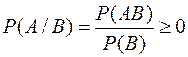 .
.
2) Событие А при условии наступления события В будет достоверным, если 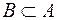 .
.
Действительно: 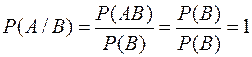 .
.
3) Если А1, А2, …, Аn попарно несовместны, то
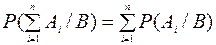
Дата добавления: 2021-12-14; просмотров: 592;











