Решение дифференциальных уравнений САУ

Линеаризация и приведение к типовой форме дают временное уравнение динамики системы в общем виде

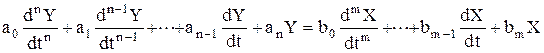, (1.2.8)

где a₀, a₁,...a_n-1, a_n - коэффициенты при производных выходного параметра Y;

b₀,...b_m-1, b_m - коэффициенты при производных входного параметра.

Классический метод решения уравнения (1.2.8) заключается в получении аналитического выражения общего интеграла уравнения, который определяется суммой

Y(t) = Y_вын + Y_св(t), (1.2.9)

где Y(t) - общее решение, дающее переходной процесс выходной величины в функции времени;

Y_вын - частное решение уравнения, определяющее вынужденное (установившееся) движение для производных равных нулю;

Y_св(t) - решение левой части уравнения (1.2.8), приравненное нулю (характеризует свободное движение).

В частном случае, когда корни характеристического уравнения l_i вещественные для характеристического уравнения

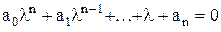, (1.2.10)

получим

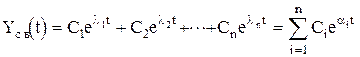, (1.2.11)

где C_i - постоянные интегрирования, l_i - корни характеристического уравнения (1.2.10).

Если корни l_i мнимые, то в решении (1.2.11) будут и гармонические составляющие, т.е. будет происходить колебательный процесс.