Дифференциальные уравнения САУ

Динамическое состояние системы можно представить в виде совокупности дифференциальных уравнений, описывающих все физические процессы - механические, электрические, электромагнитные и др., происходящие в элементах (звеньях) системы.

Для исследования же системы удобнее иметь одно общее дифференциальное уравнение, составленное на основе уравнений каждого из входящих в нее отдельных звеньев путем исключения промежуточных переменных, при этом за входную и выходную переменные каждого из них необходимо принимать те, которые указаны в функциональной схеме исследуемой системы.

При составлении и решении уравнений динамики системы следует учитывать, что коэффициенты дифференциального уравнения САУ зависят от параметров звеньев (например, момента инерции, массы, емкости, индуктивности и т.п.).

Рассмотрим механическую систему при неравномерном движении.

Если скорость какого-либо тела постоянна, то расстояние будет равно

S(t) = S₀ + Vt или Y(t) = Y₀ + t, (1.2.1)

где Y(t) = S - расстояние, пройденное телом за время t;
=V - скорость тела при движении;
Y₀ = S₀ - расстояние пройденное телом до начала отсчета t=0.

Если же еще и скорость непостоянна, то в общем случае расстояние будет равно

или , (1.2.2)

где - ускорение при движении.

При нескольких переменных в общем виде уравнение динамики звена или САУ имеет вид

, (1.2.3)

где , ... - управляемая переменная и ее производные;
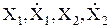, ...- входные переменные и их производные;
, ...- возмущающее воздействие и его производная.

С учетом принципа суперпозиции для линейных систем при независимых друг от друга X₁, X₂ и F можно записать

. (1.2.4)

Пример. Составим дифференциальное уравнение протекания тока через обмотку возбуждения двигателя (рис.1.2.2).

,

где L - индуктивность; i - ток; U - напряжение; R - сопротивление обмоток.

Линеаризация САУ

В общем случае САУ нелинейны, т.е. хотя бы в одном звене имеется нелинейная характеристика. Решение дифференциальных уравнений нелинейного вида типа (1.2.3) представляет большую трудность. Поэтому необходимо произвести линеаризацию нелинейных характеристик реальных звеньев.

Линеаризацией называют замену нелинейного уравнения Y=f(t) приближенно линейным Y»KX.

Основой линеаризации является выдвинутое П.А. Вышнеградским предложение, что в течение всего процесса управления имеют место достаточно малые отклонения всех переменных от их установившегося значения. Это дает возможность линеаризовать нелинейную функцию в окрестности точки установившегося равновесия. Такую линеаризацию осуществляют методом А.М. Ляпунова. Линеаризацию по Ляпунову проводят в окрестности установившегося состояния с последующим отбрасыванием нелинейного остатка разложения Х.

Разложим непрерывную нелинейную функцию f(X) в ряд Тейлора

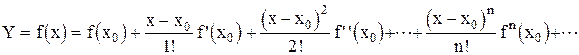(1.2.5)

Если ограничиться первым приближением линеаризации, то получим линейное уравнение относительно DX

, (1.2.6)

где - угол наклона зависимости в точке X₀ (рис.1.2.1).

Рис.1.2.1. Линеаризация дифференциальных уравнений САУ

Часто уравнения нужно записывать в приращениях:

f(X)=f₀(X₀)+f(DX) или

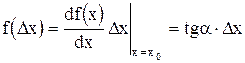. (1.2.7)

Для того, чтобы привести уравнения к единому безразмерному виду, проводят нормирование и получают уравнения в относительных единицах. Нормирование осуществляют путем деления на базовое значение или номинальную величину 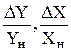. В этом случае эти величины можно сравнивать качественно и количественно.