Деление целых чисел с остатком
Объектами нашего изучения будут множества N = {1, 2, 3, 4, … } всех натуральных чисел и Z = { … , –3, –2, –1, 0, 1, 2, 3, … } – всех целых чисел с естественными операциями сложения + и умножения × . Условимся обозначать через N0 множество N È {0}.
Пусть a, b Î Z и a = b×q + r для некоторых целых чисел q, r, причём 0 £ r < |b|. Тогда говорят, что q является (неполным) частным от деления a на b, r – остатком от деления a на b, а саму запись a = b×q + r называют формулой деления с остатком числа a на b. Если r = 0, то говорят, что a делится нацело на b, число b в этом случае называют делителем числа a, а число a – кратным числа b и пишут a  b или b | a. Записи a
b или b | a. Записи a 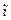 b и b
b и b 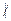 a означают, что a не делится нацело на b.
a означают, что a не делится нацело на b.
Замечание: формула деления с остатком определена только для b 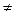 0, ибо условие 0 £ r < |b| противоречиво в случае b = 0.
0, ибо условие 0 £ r < |b| противоречиво в случае b = 0.
Примеры: 1.–2, –1, 1, 2 – все возможные делители числа 2,
2.21 = (–4)×(–5) + 1 – формула деления с остатком числа 21 на –4 (q = –5, r = 1),
3.–21 = 4×(–5) – 1 – этоне формула деления с остатком, т.к. остаток должен быть неотрицательным.
Теорема (о делении целых чисел с остатком).Для любых целых чисел a, b 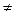 0 однозначно определены частное q и остаток r от деления a на b (т.е. " a Î Z " b Î Z \ {0} $ ! q, r Î Z a = b×q + r Ù 0 £ r < |b|).
0 однозначно определены частное q и остаток r от деления a на b (т.е. " a Î Z " b Î Z \ {0} $ ! q, r Î Z a = b×q + r Ù 0 £ r < |b|).
Доказательство. I. Существование частного и остатка.Разберём случай неотрицательных чисел a, b. Если a < b, то a = b×0 + a (0 £ a < b) – формула деления с остатком.
Если же a ³ b, то изобразив отрезки длины a и b на числовой оси, и последовательно прикладывая отрезки длины b друг к другу, найдём такое

 натуральное q ³ 1, что q×b £ a < (q+1)×b. Положим r = a – q×b и заметим, что ввиду выбора q, 0 £ r < b , а также a = b×q+r, т.е. q – частное, а r – остаток от деления b на a.
натуральное q ³ 1, что q×b £ a < (q+1)×b. Положим r = a – q×b и заметим, что ввиду выбора q, 0 £ r < b , а также a = b×q+r, т.е. q – частное, а r – остаток от деления b на a.
Итак, для неотрицательных целых чисел существование деления с остатком доказано.
Если теперь a > 0, b < 0, и a = |b|×q + r – найденная формула деления с остатком положительных чисел, то 0 £ r < |b|,и значит, a = b×(–q) + r – искомая формула деления с остатком. Аналогичны рассуждения и в оставшихся случаях. Например, если a < 0, b > 0 и –a = b×q + r, где 0 £ r < b, то при r = 0 искомая формула принимает вид a = b×(–q) + 0, а при r > 0 имеем a = b×(–q) – r = b×(–q)–b+b – r = b×(–q–1)+(b–r), причём 0 < b – r < b, т.е. –q – 1, b – r – искомые частное и остаток соответственно. Случай a < 0, b < 0 оставляется в качестве упражнения.
II. Единственность частного и остатка.Докажем теперь единственность частного и остатка. Пусть a = b×q1 + r1 = b×q2 + r2 – две формулы деления с остатком, т.е. 0 £ ri < |b| (i = 1, 2). Тогда b×(q1 – q2) = r2 – r1 , и переходя к модулям: |b|×|q1 – q2| = |r2 – r1| .
 Если q1 = q2 , то r2 = r1 и всё доказано. Если же q1 ¹ q2 , то |q1 – q2| Î N и |b|×|q1 – q2| ³ |b|. С другой стороны, из рисунка слева видно, что |r1 – r2|< rj < |b| . Таким образом, |b| £ |b|×|q1 – q2| = = |r1 – r2| < |b| – противоречие, которое показывает, что случай q1 ¹ q2 невозможен.
Если q1 = q2 , то r2 = r1 и всё доказано. Если же q1 ¹ q2 , то |q1 – q2| Î N и |b|×|q1 – q2| ³ |b|. С другой стороны, из рисунка слева видно, что |r1 – r2|< rj < |b| . Таким образом, |b| £ |b|×|q1 – q2| = = |r1 – r2| < |b| – противоречие, которое показывает, что случай q1 ¹ q2 невозможен.
Теорема доказана.
q-чные системы счисления
Записывать натуральные числа можно по-разному, у разных народов существуют свои особенные формы записи чисел. Наиболее употребительна в настоящее время десятичная форма представления чисел, в которой натуральное число, однозначно представимое в виде
an  10n + an-1
10n + an-1  10n-1 + … + a1
10n-1 + … + a1  10 + a0 ,
10 + a0 ,
где 0 £ ai £ 9 (0 £ i £ n), an > 0, кратко записывается символически в виде последовательности десятичных (арабских) цифр: 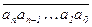 (черта здесь использована для того, чтобы отличать последовательность цифр записываемого произвольного числа от произведения an
(черта здесь использована для того, чтобы отличать последовательность цифр записываемого произвольного числа от произведения an  an-1
an-1  …
…  a1
a1  a0 ,и в каждом конкретном случае не ставится). Так, 123 = 1×102+2×10+1, 47 = 4×10 + 7, 5709 = 5×103+7×102+0×10+9.
a0 ,и в каждом конкретном случае не ставится). Так, 123 = 1×102+2×10+1, 47 = 4×10 + 7, 5709 = 5×103+7×102+0×10+9.
Другим употребительным способом записи натуральных чисел является запись с помощью римских цифр. Так, 123 =100+10+10+1+1+1 = СХХIII , где цифра С обозначает число 100, Х – соответственно 10, I – 1. Кроме использованных цифр в такой записи чисел могут участвовать цифры V – 5, L – 50, D – 500, M – 1000. Для экономии символов в римской записи предусмотрены специфические правила, подробное обсуждение которых не входит в наши планы. Например,
47 ¹ ХХХХVII = 10+10+10+10+5+1+1, 47 = XLVII = (50–10)+5+1+1,
5709 ¹ MMMMMDССIIIIIIIII,
5709 = МММММDCCIX (= 5´1000+500+ +2´100 +(10–1)).
Разница между этими системами записи чисел заключается в том, что в первой значение каждой цифры изменяется в зависимости от её позиции – она может обозначать количество единиц, количество десятков, сотен, тысяч, и.т.д., – а во второй цифра сохраняет своё значение независимо от позиции. Системы записи первого типа называются позиционными системами счисления, а системы второго типа – непозиционными.
Как будет доказано ниже, каждое натуральное число можно однозначно разложить не только по степеням числа 10, но и по степеням любого наперёд заданного натурального числа q > 1. Этим оправдано следующее определение: говорят, что натуральное число k записано в виде систематического числа ( 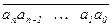 )q в позиционной q-чной системе счисления (скобки и черта в конкретных случаях не ставятся), если
)q в позиционной q-чной системе счисления (скобки и черта в конкретных случаях не ставятся), если
k = an×qn + an–1×qn–1 + … + a1×q + a0 ,
где числа ai удовлетворяют условиям 0 £ ai < q (0 £ i £ n – 1), an > 0 и называются цифрами числа n в рассматриваемой q-чной системе счисления. Если q > 10, то для обозначения цифр, бо¢льших 9, используют круглые скобки или последовательные начальные буквы латинского алфавита: например, (10) или A обозначает цифру 10, (11) или B – цифру 11, (12) или С – цифру 12, а (17) или H – обозначает цифру 17.
Примеры: 1.12310 = 1738 = 7B16 = 11110112 , т.к.
12310 = 1×102 + 2×10 + 3 = 1×82 + 7×8 + 3 =
= 7×16 + 11 = 1×26 + 1×25 + 1×24 + 1×23 + 0×22 + 1×2 + 1.
2.570910 = 131158 = 164(13)16 = 164D16 = 10110010011012 = 105709 .
Теорема (о q-чных позиционных системах счисления). Любое натуральное число обладает единственным представлением в виде систематического числа 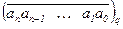 в позиционной системе счисления с произвольным натуральным основанием q > 1.
в позиционной системе счисления с произвольным натуральным основанием q > 1.
Доказательство. Необходимо доказать, что для любого натурального числа k найдутся однозначно определённые цифры a0 , … , an (0 £ ai < q , 0 £ i £ n – 1, an > 0) со свойством k = an×qn + an–1×qn–1 + … + a1×q + a0 .
Ясно, что k = (an×qn–1 + an–1×qn–2 + … + a1)×q + a0 и 0 £ a0 < q, т.е. a0 – остаток от деления числа k на q, а an×qn–1 + an–1×qn–2 + … + a1 = k0 – частное, которые определены однозначно.
Аналогично имеем: k0 = (an×qn–2 + an–1×qn–3 + … + a2)×q + a1 = k1×q+a1 и q-чная цифра a1 – это остаток от деления числа k0 на q. Продолжая этот процесс, находим:
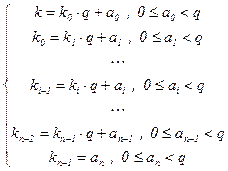
При этом обязательно найдётся такое n Î N0 , что kn–1 < q: действительно, если ki ³ q , то, по построению, k > k0 > k1 > … – бесконечная убывающая цепочка натуральных чисел, что невозможно. Итак, эти формулы однозначно определяют q-чные цифры a0 , … , an числа k.
Теорема доказана.
Позиционные системы счисления с основаниями, не равными 10, широко используются в различных областях человеческой деятельности. В частности, в информатике для представления чисел в ЭВМ применяется двоичная система счисления, а для визуализации двоичных чисел часто применяются более экономные 8-ричная и 16-ричная системы счисления.
Обилие систем счисления с различными основаниями требует умения переводить числа из одной системы счисления в другую.
Перевод числа из десятичной системы счисления в q-ичную
Описанный выше алгоритм нахождения q-чных цифр на практике реализуют в виде последовательного деления в столбик.
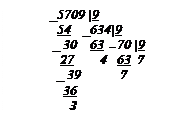 Пример:Найти запись числа 5709 в девятиричной системе счисления.
Пример:Найти запись числа 5709 в девятиричной системе счисления.
Оформим вышеописанный процесс в виде деления в столбик: 5709 = 77439 .
Перевод числа из десятичной системы счисления в произвольную q-чную легко программируется: все вычисления осуществляются в одном цикле.
Перевод числа из q-чной системы счисления в десятичную
(схема Горнера)
Если k = ( 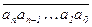 )q , то k = an×qn + an–1×qn–1 + … + a1×q + a0 = = ((…((an×q + an–1)×q + an–2)×q … )×q + a1)×q + a0 . Таким образом, процесс нахождения десятичной записи числа k можно организовать рекуррентно, полагая
)q , то k = an×qn + an–1×qn–1 + … + a1×q + a0 = = ((…((an×q + an–1)×q + an–2)×q … )×q + a1)×q + a0 . Таким образом, процесс нахождения десятичной записи числа k можно организовать рекуррентно, полагая 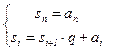 (n–1 ³ i ³ 0). Записывая каждое si в десятичной системе счисления, в результате получим десятичную запись числа k = s0 . Описанный выше процесс вычислений называется схемой Горнера.
(n–1 ³ i ³ 0). Записывая каждое si в десятичной системе счисления, в результате получим десятичную запись числа k = s0 . Описанный выше процесс вычислений называется схемой Горнера.
Пример:Найти десятичную запись числа 1С8D16 . Оформим процесс вычислений по схеме Горнера в виде таблицы:
| i | 3 | 2 | 1 | 0 |
| ai | 1 | 12 | 8 | 13 |
| si | 1 | 28 = 1´16+12 | 456 = 28´16+8 | 7309 = 456´16+13 |
Таким образом, 1С8D16 = 730910 .
Следует отметить, что схему Горнера можно применять для вычисления любых полиномиальных выражений вида an  xn + an–1
xn + an–1  xn–1 + … + a1
xn–1 + … + a1  x + a0 , где ai (0 £ i £ n) и x – числа, матрицы и другие математические объекты, которые можно складывать и умножать.
x + a0 , где ai (0 £ i £ n) и x – числа, матрицы и другие математические объекты, которые можно складывать и умножать.
Дата добавления: 2021-12-14; просмотров: 434;











