Простейшие свойства взаимно простых чисел

1⁰. Если D = НОД(а₁ , … , а_п), то целые числа 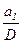, … , 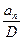взаимно просты в совокупности.

В самом деле, если a_i = D×b_i (1 £ i £ n), то числа b₁ , … , b_n не могут иметь неединичного положительного общего делителя (?!), т.е. являются взаимно простыми в совокупности.

2⁰. Целые числа а₁ , … , а_п взаимно просты в совокупности тогда и только тогда, когда существуют целые числа х₁ , … , х_п со свойством а₁×х₁ + … + а_п×х_п = 1.

Действительно, если числа взаимно просты в совокупности, то можно записать линейное разложение НОД(а₁ , … , а_п) = 1 = а₁×х₁ + … + а_п×х_п .

Обратно, если существуют целые числа х₁ , … , х_п с указанным свойством а₁×х₁ + … + а_п×х_п = 1, то любой общий делитель а₁ , … , а_п очевидно делит 1, так что НОД(а₁ , … , а_п) = 1.

Из свойства 2⁰ легко вывести следующие два свойства:

3⁰. Целые числа а и b взаимно просты тогда и только тогда, когда существуют целые числа х, у со свойством а×х + b×y = 1.

4⁰. Целые числа а₁ , … , а_п попарно взаимно просты тогда и только тогда, когда для любых i < j (1 £ i, j £ n) существуют целые числа x , y со свойствами а_i×х + a_j×y = 1.

5⁰. Для целых чисел a, b, т следующие два условия эквивалентны:

(1) а взаимно просто с т и b взаимно просто с т,

(2) произведение а×b взаимно просто с т.

(1) Þ (2) По свойству 3⁰ найдутся целые числа х, у, u, v со свойствами a×x + m×y = 1, b×u + m×v = 1. Перемножая эти равенства получим:

1 = (a×x+m×y)×(b×u+m×v) = (a×b)×x×u + m×(a×x×v + b×y×u + m×y×v),

что и требовалось.

(2) Þ (1) Если a×b×x + m×y = 1, то это равенства показывает ввиду свойства 3⁰, что а взаимно просто с т и b взаимно просто с т.

6⁰. Для целых чисел a₁ , … , а_п , т следующие два условия эквивалентны:

(1) каждое число а_i взаимно просто с т (1 £ i £ n),

(2) произведение а₁× … ×a_n взаимно просто с т.

Это доказывается индукцией по п. Базу индукции (п = 2) обеспечивает свойство 5⁰. Предположим, что эквивалентность условий уже доказана для п = k ³ 2 и докажем её для п = k + 1. Имеем

(каждое число а_i взаимно просто c m (1 £ i £ k+1)) Û

Û (а_i взаимно просты с т (1 £ i £ k) и a_k+1 взаимно просто с т)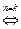

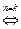(а₁× … ×a_k взаимно просто с т и a_k+1 взаимно просто с т)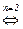

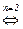(произведение (а₁× … a_k)×a_k+1 взаимно просто с т),

что и требовалось доказать.

7⁰. Если целые числа a и b взаимно просты, то

" с Î Z a | b×c Û a | c.

В самом деле, если b×c = а×d, то учитывая существование целых чисел х, у со свойством а×х + b×y = 1, получим

с = а×c×x + b×c×y = а×c×x + a×d×y = a×(c×x + d×y).

Обратная импликация очевидна.

Это свойство часто используется в теоретико-числовых рассуждениях, с его помощью можно, например, сократить доказательства некоторых свойств делимости нацело. Поэтому будем его называть основным свойством взаимно простых чисел.

Упражнения: 1. Проанализируйте доказательства свойств делимости нацело и упростите некоторые из них, применив свойство 7⁰.

2.Докажите, что если квадрат некоторого натурального числа раскладывается в произведение попарно взаимно простых множителей, то каждый из них является квадратом подходящего натурального числа.

3.Докажите, что если D = НОД(а, b), то " п Î N Dⁿ = НОД(аⁿ, bⁿ).

Простые числа

Натуральное число p называется простым, если оно имеет ровно два различных между собой натуральных делителя: 1 и p. Натуральное число, большее единицы, называется составным, если оно не является простым.

Примеры:1.2, 3, 5, 37, 101 – простые числа,

2.4, 6, 8, 9, 123, 1024 – составные числа,

3.числа–7, –128, –1024 – не являются ни простыми, ни составными,

4.числа 0, +1, –1 – не являются ни простыми, ни составными.

Таким образом, любое натуральное число либо равно единице, либо является простым, либо – составным. Аналогично, множество всех целых чисел разбивается на пять непересекающихся подмножеств – множество всех простых чисел, множество всех составных чисел, множество чисел противоположных простым, множество чисел противоположных составным и множество {–1, 0, +1}.

Простые числа обладают многими удивительными и загадочными свойствами. В качестве примера упомянем следующую, ещё не решённую задачу. Рассмотрим бесконечную таблицу чисел слева. В ней первая строка состоит из последовательных простых чисел, а числа остальных строк получены из стоящих непосредственно слева и справа над ними взятием модуля разности. Верно ли, что в начале каждой строки первой будет стоять единица ?