Простые числа в арифметических прогрессиях

<4 5 678 9 10 >

Займёмся теперь выяснением вопроса о количестве простых чисел. Следующая теорема впервые появилась в “Началах” Евклида и имеет множество различных доказательств, из которых приведём лишь одно.

Теорема (Евклида о бесконечности числа простых чисел). Простых чисел бесконечно много.

Доказательство.Предположим, вопреки доказываемому, что множество простых чисел конечно и состоит из элементов p₁ = 2 < p₂ = 3 < … < p_n . Рассмотрим число N = p₁×p₂× … ×p_n + 1 > 1. Оно, с одной стороны, раскладывается в произведение простых множителей (по основной теореме арифметики), а с другой – не может делиться ни на одно из простых чисел p_i (1 £ i £ n): если p_i | N , то p_i | (N – p₁× … ×p_i× … ×p_n) = 1) – противоречие.

Теорема доказана.

Эта теорема утверждает бесконечность числа простых чисел в арифметической прогрессии 1 + 1×n (n Î N₀). Конечно, есть арифметические прогрессии a + b×n (n Î N₀), в которых совсем нет простых чисел: такова, например, прогрессия 4 + 4×n (n Î N₀), в которой каждое число делится на 4.

Вообще, если D = НОД(a, b), то на D делится любой член последовательности a + b×n (n Î N₀), так что при составном D в такой арифметической прогрессии нет ни одного простого числа. Если D = p – простое, то любое число прогрессии делится на p, так что она может содержать только простое число p. Эта возможность реализуется только в том случае, когда a₁ + b₁×k = 1, где 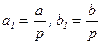при некотором k Î N₀. Например, прогрессия 49 + 7×n (n Î N₀) не содержит простых чисел, а прогрессия 7 – 42×n (n Î N₀) содержит простое число 7.

Условие a₁ + b₁×k = 1 будет выполнено для некоторого k Î N₀ тогда и только тогда, когда либо a₁ = 1, либо a₁ – 1 M b₁ и (a₁ – 1)×b₁ < 0. Таким образом, доказана

Теорема (об арифметических прогрессиях с малым числом простых). Если D = НОД(a, b) > 1, то арифметическая прогрессия a + b×n (n Î N₀) содержит единственное простое число р в случае D = p = a или, если D = p, a₁ – 1 M b₁ , (a₁ – 1)×b₁ < 0. Если D составное число, то в арифметической прогрессии нет простых чисел.

Остаётся вопрос о количестве простых чисел в арифметической прогрессии a + b×n (n Î N₀) со взаимно простыми начальным членом a и разностью b. Оказывается, имеет место следующая удивительная теорема:

Теорема (Дирихле). Любая арифметическая прогрессия вида a + b×n (n Î N₀) со взаимно простыми a, b содержит бесконечно много простых чисел.

Без доказательства.

Примеры: 1.Арифметическая прогрессия 1 + 2×n (n Î N₀) содержит все нечётные простые числа.

2. Любое простое число, большее 3, при делении на 3 даёт остаток 1 или 2. По этому одна из арифметических прогрессий 1 + 3×n или 2 + 3×n (n Î N₀) содержит бесконечно много простых чисел (на самом деле, конечно, обе !). На самом деле любое простое число p > 3 можно записать в виде 3×n ± 1 (n Î N₀). Это очевидно дляпростого числа p из арифметической прогрессии 1 + 3×n (n Î N₀), а p = 2 + 3×n = 3 – 1 + 3×n = 3×(n+1) – 1, что и требовалось.

3. Любое простое число, большее 3, при делении на 4 даёт остаток 1 или 3 (остатки 0, 2 не могут встретиться, поскольку числа вида 4×q, 4×q + 2 являются чётными). Таким образом, одна из арифметических прогрессий 1 + 4×n или 3 + 4×n (n Î N₀) содержит бесконечно много простых чисел (по теореме Дирихле – обе !). На самом деле любое простое число p > 3 можно записать в виде 4×n ± 1 (n Î N₀). Это очевидно дляпростого числа p из арифметической прогрессии 1 + 4×n (n Î N₀), а p = 3 + 4×n = = 4 – 1 + 4×n = 4×(n+1) – 1, что и требовалось.

4.Любое простое число, большее 5, при делении на 6 даёт остатки 1 или 5 (остатки 0, 2 и 3 не могут встретиться, поскольку числа вида 6×q, 6×q + 2 и 6×q + 3 делятся на 2 и на 3 соответственно). Таким образом, одна из арифметических прогрессий 1 + 6×n или 5 + 6×n (n Î N₀) содержит бесконечно много простых чисел (по теореме Дирихле – обе !). На самом деле любое простое число p > 5 можно записать в виде 6×n ± 1 (n Î N₀). Это очевидно дляпростого числа p из арифметической прогрессии 1 + 6×n (n Î N₀), а p = 5 + 6×n = 6 – 1 + 6×n = 6×(n+1) – 1, что и требовалось.

Теорема (о простых числах в арифметических прогрессиях 4×n – 1, 6×n – 1). Арифметические прогрессии 4×n – 1 , 6×n – 1 (n Î N₀) содержат бесконечно много простых чисел.

Доказательство. Проведём рассуждения от противного одновременно для обеих указанных прогрессий вида b×n – 1 (n Î N₀), где b Î {4, 6},применив идею доказательства Евклида бесконечности простых чисел.

Предположим, вопреки доказываемому, что данная арифметическая прогрессия содержит конечное число простых членов p₁ < p₂ < … < p_k и рассмотрим число N = b×p₂×…×p_k – 1 из этой прогрессии. По основной теореме арифметики, оно раскладывается в произведение простых множителей. Эти простые множители нечётны (т.к. b чётно) и не могут совпадать ни с одним из чисел p₂ , … , p_k : в противном случае –1 = N – b×p₂×…×p_k делилось бы на одно из чисел p₂ , … , p_k , что невозможно. Поскольку каждое нечётное простое число равно 3 или имеет вид b×n ± 1 (по приведённой выше классификации остатков простых чисел), то в разложении числа N могут участвовать только простые множители вида b×n + 1 (объясните, почему число N не делится на 3 ?!). Однако, произведение чисел вида b×n + 1 снова имеет этот же вид: (b×n + 1)×( b×m + 1) = b×s + 1, где s = n + m + b×n×m , и не может дать число b×n – 1 (?!).

Теорема доказана.

Примеры: 1. Найти все простые числа p, для которых p – 2, p + 3 простые.

Таких чисел нет, т.к. p = 2 не годится, а для нечётного p число p + 3 делится на 2.

2. Найти все простые числа p, для которых p + 2, p + 4 простые.

Ясно, что p = 3 годится, а p = 2 – нет. Если p > 3, то p = 3×n ± 1. Если p = 3×n + 1, то p + 2 = 3×n + 3 M 3. Если же p = 3×n – 1, то p + 4 = 3×n + 3 M 3.

3. Докажите, что для любого нечётного простого числа p > 3 число p² – 1 делится на 24.

Нужно доказать, что p² – 1 M 3 и p² – 1 M 8. Запишем p² – 1 = (p+1)×(p–1) и заметим, что для p = 3×n ± 1 одна из скобок делится на 3. Аналогично для p = 4×n ± 1 одна из скобок делится на 4, а другая – на 2.

О распределении простых чисел

Для каждого положительного действительного числа x обозначим через 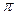(x) количество простых чисел в интервале (–¥, x]. Таким образом, получаем отображение p : R 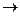N (называемое функцией Чебышева), значение которого можно вычислить для любого конкретного x Î R. Например, p(x) =0 при x < 2, p(2) = 1 = p(2,99), p(3) = 2, p(10) = 4 = p(7,001). Возникает вопрос о поведении функции p(x), более точно – о её порядке роста. Ограничимся только формулировками самых ранних и простых (но далеко не очевидных) результатов на эту тему:

Теорема (неравенства Чебышева). (1) Существуют такие константы 0 < a < 1 < b (например, годятся a = 0,92129, b = 1,0555), что для всех достаточно больших значений x Î R верны неравенства

.

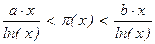Эта теорема была доказана в 1850 г. Кроме того, П.Л.Чебышевым было доказано, что если существует 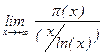, то он равен 1. Существование же этого предела удалось доказать только спустя полвека, используя теорию функций комплексного переменного.

Теорема (Адамар, Валле-Пуссен) Предел 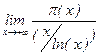существует и равен 1 (асимптотический закон распределения простых чисел).

В той же основополагающей работе П.Л.Чебышева, было дано доказательство следующей известной гипотезы

Теорема (постулат Бертрана). Для любого натурального числа n на отрезке [n; 2×n] содержится хотя бы одно простое число.

В то же время, как показывает следующая теорема, существуют сколь угодно длинные отрезки, не содержащие простых чисел.

Теорема (о сколь угодно длинных отрезках, не содержащих простых чисел). Для любого натурального п на отрезке [п! + 2, п! + п] нет ни одного простого числа.

Доказательство. Любое число из рассматриваемого отрезка имеет вид п! + k, где 2 £ k £ n , и делится на k.

Теорема доказана.

Хотя современная теория чисел продвинулась далеко вперёд, многие вопросы о простых числах остаются нерешёнными и по сей день. Например, до сих пор неизвестно – конечны ли множества простых чисел вида 1 + n² и 1 + 2ⁿ (n Î Z).

Язык сравнений

Пусть a, b, m Î Z и m ¹ 0. Говорят, что числа a и b сравнимы по модулю m, если разность a – b делится нацело на m: a º b (mod m). Таким образом, a º b (mod m) Û $ t Î Za – b = m×t.

Примеры: 1. 5 º 17 (mod 6), т.к. 5 – 17 = –12 = 6×(–2),

3 º –5 (mod 4), т.к. 3 – (–5) = 8 = 4×2,

2. –3 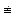–2 (mod 5), т.к. –3 – (–2) = 1 и 5 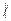1,

28 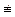15 (mod 3), т.к. 28 – 15 = 13 и 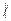3 13.

Свойства сравнений

1⁰. Числа a и b сравнимы по модулю m тогда и только тогда, когда они дают одинаковые остатки при делении на m.

Действительно, если a º b (mod m), а r и s – остатки от деления a и b на m соответственно, то a = m×q + r, b = m×p + s, 0 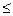r < |m|, 0 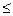s < |m| , причём a – b = m×(q – p) + (r – s) делится нацело на m. Это возможно лишь в том случае, когда m | (r – s), т.е. r = s (поскольку –m < r – s < m).

Обратно, есличисла a и b дают одинаковые остатки при делении на m, то a = m×q + r, b = m×p + r, 0 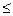r < m. Поэтому a – b = m×(q – p) кратно m , что и требовалось доказать.

Следующие три свойства следуют из 1⁰.

2⁰. Условия a M b и a º 0 (mod b) эквивалентны.

В самом деле, a M b Û a – 0 M b Û a º 0 (mod b).

3⁰. Любое целое число a сравнимо само с собой по любому модулю m (рефлексивность отношения сравнимости).

4⁰. Если a º b (mod m), то b º a (mod m) (симметричность отношения сравнимости).

5⁰. Если a º b (mod m) и b º с (mod m), то a º c (mod m) (транзитивность отношения сравнимости).

Вместе свойства 2⁰-3⁰ дают

6⁰. Если a º b (mod m), то для любого целого числа c справедливо

a ± c º b ± c (mod m) , a×c º b×c (mod m).

В самом деле, если a – b = m×t, то (a ± c) – (b ± c) = a – b = m×t и аналогично a×c – b×c = (a – b)×c = m×t×c.

7⁰. Если a º b (mod m) и c º d (mod m), то a ± c º b ± d (mod m).

Действительно, если a – b = m×t , c – d = m×s , то

(a ± c) – (b ± d) = (a – b) ± (c – d) = m×t – m×s = m×(t – s).

8⁰. Если a º b (mod m) и c º d (mod m), то a×c º b×d (mod m).

В самом деле, если a – b = mt , c – d = ms, то

(a×c) – (b×d) = a×с – b×с + b×c – b×d = (a – b)×c + b×(c – d) =

= mt×c – b×ms = m× (tc – bs).

9⁰. Если a º b (mod m), то для любого натурального k верно сравнение a^k º b^k (mod m).

При k = 1 сравнение верно по условию. Отсюда последовательно получаем, умножая на то же сравнение a º b (mod m):

a² º b² (mod m), a³ º b³ (mod m), … , a^k º b^k (mod m).

10⁰. Если целые числа a, b, m делятся нацело на число d Î Z\ {0}, то a º b (mod m) тогда и только тогда, когда .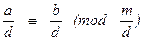

Действительно, если a = d×a₁, b = d×b₁ , m = d×m₁ ,то

a – b = m×t Û a₁ – b₁ = m₁×t .

11⁰. Если d×a º d×b (mod m) и НОД(d , m) = 1, то a º b (mod m).

В самом деле, если d×a – d×b = m×t , то d | m×t . Поскольку числа d и m взаимно простые, то по основному свойству взаимно простых чисел d | t , т.е. t = d×t₁ для некоторого целого t₁ . Значит, a – b = m×t₁ .

Сравнения дают удобный язык для изучения делимости чисел. Связь сравнений с делимостью выявлена в свойстве 2⁰.

Примеры: 1. Докажите, что если a при делении на 23 даёт остаток 5, то a⁴ – 8×a³ + 19 даёт остаток .

Действительно, если a º 5 (mod 23), то

a⁴ – 8×a³ + 19 º (a²)² – 8×a×a² + 19 º 2² – 8×5×2 + 19 º

º – 40×2 + (2² + 19) º –(–6)×2 + 0 º 12 (mod 23),

т.е. остатком будет 12.

2. Вычислить 18¹⁰⁰ + 20 (mod 25).

18¹⁰⁰ + 20 º (–7)²⁵ – 5 º –(7²)¹²×7 – 5 º –7×(–1)¹² – 5 º

º –7 – 5 º –12 º 13 (mod 25).

Функция Эйлера

Для натурального n обозначим через j(n) количество взаимно простых с n натуральных чисел на отрезке [0, n – 1]. Таким образом, получается функция j: N® N, называемая функцией Эйлера.

Примеры: 1.Найдём j(1). Отрезок [0; 1–1] = [0; 0] содержит единственное целое число 0, которое взаимно просто с n = 1

Таким образом, j(1) = 1.

2. Найдём j(2). Для этого рассмотрим отрезок [0; 2–1] = [0; 1], содержащий два целых числа 0, 1, и посчитаем количество взаимно простых с n = 2 чисел в нём:

а	0
НОД(a, 2)	2	1

Таким образом, j(2) = 1.

3. Найдём j(3). Для этого рассмотрим отрезок [0; 3–1] = [0; 2], содержащий три целых числа 0, 1, 2, и вычислим количество взаимно простых с n = 3 чисел в нём:

а	0
НОД(a, 3)	3	1	1

Таким образом, j(3) = 2.

4. Найдём j(6). Для этого рассмотрим отрезок [0; 6–1] = [0; 5], содержащий шесть целых чисел 0, 1, 2, 3, 4, 5, и вычислим количество взаимно простых с n = 6 чисел в нём:

а	0		2	3	4
НОД(a, 6)	6	1	2	3	2	1

Таким образом, j(6) = 2.

Теорема (о функции Эйлера). Для любого натурального числа n справедливы следующие утверждения:

(1) j(1) = 1,

(2) для простого числа p верно j(p) = p – 1,

(3) для любого простого числа p и натурального показателя a справедлива формула j(р^a) = р^a – р^a^–1 = p^a^–1×(p – 1) = p^a×(1 – ),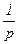

(4) функция Эйлера 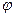мультипликативна, т.е. для любых взаимно простых чисел m и n верно j(m×n) = j(m)×j(n),

(5) если 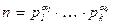, то

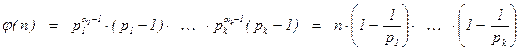Доказательство. Докажем лишь некоторые утверждения.

(1) уже доказано.

(2) Пусть p – простое число. Тогда на отрезке [0; p–1] содержатся p целых чисел: 0, 1, 2, … , p – 2, p – 1, из которых ровно одно – 0 делится на p, т.е. НОД(0, p) = p. Остальные не делятся на p, а значит НОД(a, p) = 1 (1 £ a £ p–1). Таким образом, j(p) = p – 1.

(3) Аналогично предыдущему: расположим p^a целых чисел из отрезка [0; p^a –1] в виде таблицы:

0	1	…	p–2	p–1
p	p+1	…	2×p–2	2×p–1
2×p	2×p+1	…	3×p–2	3×p–1
…	…	…	…	…
p^a–p	p^a–p+1	…	p^a–2	p^a–1

В каждом столбце все числа имеют одинаковые остатки при делении на p: числа 1-го столбца дают остаток 0, числа 2-го столбца – остаток 1, и.т.д., числа последнего столбца – остаток p – 1.

Среди этих чисел p^a чисел делятся на p только числа первого столбца, т.е. 0×p, 1×p, … , (p^a^–1 – 1)×p, НОД(s×p, p) = p (0 £ s £ p^a^–1 –1), таких чисел p^a^–1 . Остальные p^a – p^a^–1 чисел на p не делятся и взаимно просты с p^a. Таким образом, j(p^a) = p^a – p^a^–1.

(5) следует из (3) и (4):

j(n) = j( 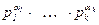) = j( 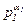)×…×j( ) =

= .

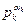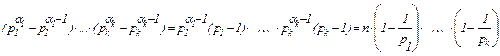Теорема доказана.

Примеры: 1.Вычислить j(15).

Находим каноническое разложение числа: 15 = 3×5. Значит,

j(15) = j(3)×j(5) = (3 – 1)×(5 – 1) = 8.

2. Вычислить j(775).

Находим каноническое разложение числа:

n_i	775	155	31	1
p_i	5	5	31
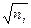
	28,…	12,…	5,…	stop

Таким образом, 775 = 5²×31. Значит,

j(775) = j(5²)×j(31) = 5×(5 – 1)×(31 – 1) = 600.

3. Вычислить j(2400).

Находим каноническое разложение числа:

n_i	2400	1200	600	300	150	75	25	5	1
p_i	2	2	2	2	2	3	5	5
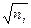
	48,…					8,…			stop

Таким образом, 2400 = 2⁵×3×5². Значит,

j(155) = j(2⁵)×j(3)×j(5²) = 2⁴×2×5×4 = 2⁷×5 = 640.

4. Решить уравнение j(x) = 12.

Пусть x = 2^a×p^b×…×q^g , где p, … , q – нечётные простые числа. Тогда при a, b , … , g > 0 получаем j(x) = 2^a^–1×(p–1)×…×(q–1)×p^b^–1×…×q^g^–1 = 12 = 2²×3. Поскольку p – 1, q – 1 чётны и a > 0, то x = 2^a×p^b (иначе показатель двойки в левой части больше 2). Ясно, что p = 3, b = 2 и a = 2, т.е. x = 2²×3².

Если a = 0, то (p–1)×…×(q–1)×p^b^–1×…×q^g^–1 = 2²×3. Если среди p, … , q нет тройки, то b = … = g = 1 и (p–1)×…×(q–1) = 2²×3. В левой части не более двух сомножителей. Если сомножитель один, то x = p = 13. Если сомножителей два, то (p–1)×(q–1) = 2²×3, т.е. p – 1 = 2×r, q – 1 = 2×s и r×s = 3. Ясно, что либо r = 1, s = 3, p = 3, q = 7, x = 21, либо r = 3, s = 1, p = 7, q = 3, x = 21.