И наименьшего общего кратного

Непосредственно из определений получаем следующие два свойства:

1⁰. Для любых не равных одновременно нулю целых чисел a₁ , … , a_n и произвольной перестановки (i₁ , … , i_n) символов 1, … , n справедливо равенство НОД(a₁ , … , a_n) = НОД( ).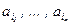

2⁰. Для любых чисел a, b Î Z, не равных одновременно нулю, справедливы равенства НОД(a, b) = НОД(–a, b) = НОД(a, –b).

Эти равенства легко следуют из общего принципа: если множества общих делителей чисел a₁ , … , a_n совпадает с множеством общих делителей чисел b₁ , … , b_m , то совпадают и наибольшие элементы этих множеств: НОД(a₁ , … , a_n) = НОД(b₁ , … , b_m).

3⁰. Для любых ненулевых целых чисел a₁ , … , a_n произвольной перестановки (i₁ , … , i_n) символов 1, … , n справедливо равенство НОК[a₁ , … , a_n] = НОК[ ].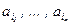

4⁰. Для любых чисел a, b Î Z \ {0} справедливы равенства НОК[a, b] = НОК[–a, b] = НОК[a, –b].

Аналогично предыдущему, всё следует из общего принципа: если множества общих кратных чисел a₁ , … , a_n совпадает с множеством общих кратных чисел b₁ , … , b_m , то совпадают и наименьшие элементы этих множеств: НОК(a₁ , … , a_n) = НОК(b₁ , … , b_m).

5⁰. Если a, b Î Z и a | b, то НОД(a, b) = |a| .

Действительно, |a| | a, |a| | b и значит, |a| £ (a, b) £ |a| , т.е. (a, b) = |a| .

6⁰. Если a, b Î Z и a | b, то НОК[a, b] = |b| .

Действительно, a | |b|, b | |b| и |b| £ [a, b] 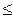|b| , т.е. [a, b] = |b| .

7⁰. Для любых чисел a, b Î Z, не равных одновременно нулю, и произвольного t Î Z справедливы равенства

НОД(a, b) = НОД(a, b – a×t) = НОД(a – b×t, b).

В самом деле, если d = (a, b), то d | a, d | b и значит, по свойствам делимости нацело, d | (b – a×t), т.е. d 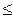(a, b – a×t) = D. Обратно, если D | a и D | (b – a×t), то D | b = (b – at) + at. Значит, D 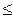d = (a, b) £ D, т.е. d = D . Второе равенство проверяется аналогично.

8⁰. Любой общий делитель d не равных одновременно нулю целых чисел а, b делит их наибольший общий делитель D = НОД(a, b).

Достаточно предполагать, что a ³ b > 0 (?!). Рассуждая от противного, выберем наименьшее натуральное число а, для которого утверждение не верно. Ясно, что a > 1, т.к. при a = 1 общими делителями чисел a, b будут только ±1 | НОД(1, b) = 1.

Рассмотрим число a₁ = a – b. По доказанным выше свойствам (a₁ , b) = = (a, b) = D , d – общий делитель чисел a₁ и b, причём 0 £ а₁ < a. Поэтому, ввиду выбора a,верно d | (a₁ , b) = D.

9⁰. Любое общее кратное K ненулевых целых чисел а, b делится на их наименьшее общее кратное k = [a, b].

Будем рассуждать от противного. Если K не делится на k , то деля с остатком, получим K = k×q + r, где 0 < r < k. Поскольку K и k – общие кратные чисел a и b, число r также является общим кратным чисел a и b (?!) вопреки минимальности наименьшего общего кратного k.

10⁰. Для любых натуральных чисел a, b справедливо равенство

НОК[a, b] = .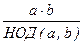

Пусть D = (a, b), a = D×a₁ , b = D×b₁ , где a₁ , b₁ – натуральные числа. Докажем, что целое число K = 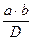= D×a₁×b₁ является наименьшим общим кратным чисел a, b. Действительно, во-первых, K = a×b₁ = b×a₁ является общим кратным чисел a, b. Во-вторых, если k – наименьшее общее кратное, то k = a×m = b×n для некоторых целых чисел m, n , причём m £ b₁ и n £ a₁ (т.к. k £ K). Пусть b₁ = m×q + r – формула деления с остатком. Тогда из a₁×m = b₁×n имеем D×a₁×r = D×a₁×b₁ – D×a₁×m×q = a×(b₁ – m×q) = b×(a₁ – n×q) делится на а и на b, т.е. является общим кратным чисел а, b. При этом D×a₁×r < D×a₁×m = k . Это возможно только при r = 0, значит, b₁ = m×q и a₁ = n×q, т.е. числа а и b делятся на D×q ³ d. Поэтому, q = 1 и K = k – наименьшее общее кратное, что и требовалось доказать.

11⁰. Для любых целых чисел a, b справедливо равенство

НОК[a, b] = .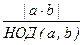

Замечание. Обобщение НОК[a₁ , … , а_n] = 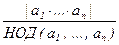доказанной формулы на случай любого числа сомножителей неверно. Придумайте контрпример и исправьте формулу.

12⁰. Для любых не равных одновременно нулю целых чисел a₁ , … , a_n–1 , a_n справедлива формула (a₁ , … , a_n) = ((a₁ , … , a_n–1), a_n).

Действительно, пусть D_n = (a₁ , … , a_n), D_n–1 = (a₁ , … , a_n–1). Тогда D_n делит все числа a₁ , … , a_n–1 , а значит, D_n | D_n–1 .Кроме того D_n | a_n , так что D_n | (D_n–1 , a_n). Поскольку (D_n–1 , a_n) – общий делитель чисел a₁ , … , a_n (?!), имеем (D_n–1 , a_n) | D_n и окончательно D_n = (D_n–1 , a_n), что и требовалось доказать.

13⁰. Для любых не равных одновременно нулю целых чисел a₁ , … , a_n–1 , a_n справедлива формула (a₁ , … , a_n) = (((…((a₁ , a₂), a₃), … ), a_n–1), a_n).

Упражнения: 1. Докажите, что

" a₁ , … , a_n Î Z \ {0} [a₁ , … , a_n] = [[a₁ , … , a_n–1], a_n],

и значит, [a₁ , … , a_n] = [[[…[[a₁ , a₂], a₃], … ], a_n–1], a_n].

2. Верно ли, что

" a, b, c Î Z \ {0} (a×c, b×c) = (a, b)×c Ù [a×c, b×c] = [a, b]×c ?

3. Верно ли, что " a, b Î Z \ {0} (a², b²) = (a, b)² Ù [a², b²] = [a, b]² ?

4. Верно ли, что " a, b, c Î Z \ {0} [(a, b), c] = c Û (a, b, c) = (a, b) ?

Алгоритм Евклида

Алгоритм Евклида применяется во многих задачах арифметики. Изучим вначале его применение для отыскания наибольшего общего делителя ненулевых целых чисел a, b. Рассмотрим теперь следующую процедуру деления целых чисел с остатком, которую и называют алгоритмом Евклида:

Шаг 0: a = b×q₀ + r₀ (0 < r₀ < b)

Шаг 1: b = r₀×q₁ + r₁ (0 < r₁ < r₀)

Шаг 2: r₀ = r₁×q₂ + r₂ (0 < r₂ < r₁)

…

Шаг i: r_i–2 = r_i–1×q_i + r_i (0 < r_i < r_i–1)

…

Шаг s: r_s–2 = r_s–1×q_s + r_s (0 < r_s < r_s–1)

Шаг s +1: r_s–1 = r_s×q_s+1 + 0 ( r_s+1 = 0 )

Алгоритм Евклида

Если b | a, то r₀ = 0 и алгоритм завершается на шаге 0, т.к. (a, b) = b. В противном случае имеем: (a, b) = (b×q₀ + r₀ , b) = (r₀ , b). Поэтому на шаге 1 делим с остатком b на r₀ . Если r₁ = 0, то (a, b) = (r₀ , b) = r₀ и алгоритм завершается. Если же r₁ > 0, то (a, b) = (r₀ , b) = (r₀ , r₀×q₁ + r₁) = (r₀ , r₁). Поэтому на шаге 3 делим с остатком r₀ на r₁ , и.т.д. В результате получается убывающая последовательность остатков:

|b| > r₀ > r₁ > … > r_i > … > > r_s > … > 0 ,

которая не может убывать бесконечно. Значит, не более чем через |b| – 1 шаг – при некотором s – получится нулевой остаток, и

(a, b) = (b, r₀) = (r₀ , r₁) = … = (r_i , r_i+1) = … = (r_s–2 , r_s–1) = (r_s–1 , r_s) = r_s .

Значит, при r₀ ¹ 0 последний делитель в алгоритме Евклида (или последний ненулевой остаток, если число шагов больше нуля) равен НОД(a, b). Таким образом, доказана следующая

Теорема (о нахождении НОД(a, b) с помощью алгоритма Евклида). Для любых ненулевых целых чисел a, b их наибольший общий делитель НОД(a, b) может быть найден с помощью алгоритма Евклида не более чем за min(|a|, |b|) – 1 шагов и равен последнему делителю в этом алгоритме (или последнему ненулевому остатку, если число шагов больше нуля).

Следствие 1 (о линейном разложении НОД(a, b)). Наибольший общий делитель НОД(a, b) любых ненулевых целых чисел a, b можно представить в виде линейной комбинации чисел a и b c целыми коэффициентами x и y: НОД(a, b) = a×x + b×y. Такое представление называется линейным разложением наибольшего общего делителя чисел a и b.

Доказательство. Будем “ползти” сверху вниз по алгоритму Евклида. Если (a, b) = |b|, то алгоритм Евклида завершается на шаге 0, и существование линейного разложения очевидно: (a, b) = a×0 + b×(±1). Если же число шагов в алгоритме Евклида больше 0, будем последовательно представлять остатки r_i в виде r_i = a×x_i + b×y_i (0 £ i £ s). В результате x = x_s , y = y_s .

Ясно, что r₀ = a×1 + b×(–q₀), так что можно положить x₀ = 1, y₀ = –q₀ . Далее, r₁ = b×1+r₀×(–q₁) = b×1+(a×1+b×(–q₀))×(–q₁) = a×(–q₁)+b×(1+q₀×q₁), т.е. x₁ = –q₁ , y₁ = 1+q₀×q₁ . Предположим, что коэффициенты x_k , y_k построены для k = 0, 1, … , i–1 < s. Тогда шаг i алгоритма Евклида даёт равенство

r_i = r_i–2 + r_i–1×(–q_i) = (a×x_i–2 + b×y_i–2)+(a×x_i–1 + b×y_i–1)×(–q_i) =

= a×(x_i–2 – x_i–1×q_i)+b×(y_i–2 – y_i–1×q_i),

и можно положить x_i = x_i–2 – x_i–1×q_i , y_i = y_i–2 – y_i–1×q_i . Таким образом, доказано не только существование представлений r_i = a×x_i + b×y_i (0 £ i £ s), но и указан явный способ вычисления чисел x_k , y_k по следующим рекуррентным формулам :

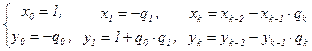(2 £ k £ s).

Следствие 1 доказано.

Следствие 2 (о линейном разложении НОД(a₁ , … , а_n)). Наибольший общий делитель НОД(a₁ , … , a_n) любых ненулевых целых чисел a₁ , … , a_n можно представить в виде линейной комбинации этих чисел c целыми коэффициентами: НОД(a₁ , … , a_n) = a₁×x₁+ …+a_n×x_n . Такое равенство называется линейным разложением НОД(a₁ , … , a_n).

Доказательство. Воспользуемся доказанной выше формулой

(a₁ , … , a_n) = (((…((a₁ , a₂), a₃), … ), a_n–1), a_n).

Если D_n = (a₁ , … , a_n) и D_n–1 = (a₁ , … , a_n–1), то D_n = (D_n–1 , a_n). Линейное разложение для D₂ = (a₁ , a₂) уже построено. Если уже построены линейные разложения

D_n–1 = a₁×u₁ + … + a_n–1×u_n–1 , D_n = D_n–1×u + a_n×v,

то, подставив первое равенство во второе, получим

D_n = D_n–1×u + a_n×v = (a₁×u₁ + … + a_n–1×u_n–1)×u + a_n×v =

= a₁×(u₁×u) + … + a_n–1×(u_n–1×u) + a_n×v –

линейное разложение НОД(a₁ , … , a_n).

Следствие 2 доказано.

Примеры: 1. Найти линейное разложение НОД(–6, 8, 34).

Имеем (–6, 8, 34) = ((–6, 8), 34) = (2, 34) = 2. При этом

(–6, 8) = 2 = (–6)×(–3) + 8×(–2), (2, 34) = 2 = 2×1 + 34×0,

(–6, 8, 34) = 2 = (2, 34) = 2×1 + 34×0 = ((–6)×(–3) + 8×(–2))×1 + 34×0 =

= (–6)×(–3) + 8×(–2) + 34×0 –

линейное разложение НОД(–6, 8, 34).

2. Найти линейное разложение НОД(–12, 16, 34).

Аналогично предыдущему, (–12, 16, 34) = ((–12, 16), 34) = (4, 34) = 2,

(–12, 16) = 4 = (–12)×(–3) + 16×(–2), (4, 34) = 2 = 4×(–8) + 34×1,

(–6, 8, 34) = 2 = (4, 34) = 4×(–8) + 34×1 = ((–12)×(–3) + 16×(–2))×1 + 34×1 =

= (–12)×(–3) + 16×(–2) + 34×1 –

линейное разложение НОД(–12, 16, 34).