Расширенный алгоритм Евклида
Полученные формулы для вычисления коэффициентов xi , yi Î Zможно представить в следующем более удобном виде:
.
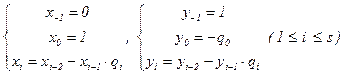Таким образом, вычисления НОД(a, b) и его линейного разложения можно провести одновременно за один цикл. Эта вычислительная процедура называется расширенным алгоритмом Евклида.
Замечание: Если на шаге 0 уже a = b×q0 , то линейное разложение тривиально: НОД(a, b) = |b| = a×0 + b×(±1), где знак + берётся для b > 0, а знак – при b < 0.
Примеры: 1. Найти линейное разложение НОД(28, –34) и вычислить НОК(28, –34).
Вычисления оформим в виде следующей таблицы:
| Шаг | А | B | Q := A / B | R := A mod B | X | Y | Проверка |
| –1 | 0 | 1 | – | ||||
| 28 | –34 | 0 | 28 | 1 | 0 | 28 = 28×1+(–34)×0 | |
| –34 | 28 | –2 | 22 | 2 | 1 | 22 = 28×2+(–34)×1 | |
| 28 | 22 | 1 | 6 | –1 | –1 | 6 = 28×(–1)+(–34)×(–1) | |
| 22 | 6 | 3 | 4 | 5 | 4 | 4 = 28×5+(–34)×4 | |
| 6 | 4 | 1 | –6 | –5 | 2 = 28×(–6)+(–34)×(–5) | ||
| 4 | 2 | 2 | 0 – stop |
Ответ: 2 = 28×(–6)+(–34)×(–5), НОК(28, –34) =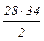 
= 476.
2.Найти линейное разложение НОД(–339, –588) и НОК(–339, –588).
| Шаг | А | B | Q := A / B | R := A mod B | X | Y | Проверка |
| –1 | 0 | 1 | – | ||||
| –339 | –588 | 1 | 249 | 1 | –1 | 249 = (–339)×1+(–588)×(–1) | |
| –588 | 249 | –3 | 159 | 3 | –2 | 159 = (–339)×3+(–588)×(–2) | |
| 249 | 159 | 1 | 90 | –2 | 1 | 90 = (–339)×(–2)+(–588)×1 | |
| 159 | 90 | 1 | 69 | 5 | –3 | 69 = (–339)×5+(–588)×(–3) | |
| 90 | 69 | 1 | 21 | –7 | 4 | 21 = (–339)×(–7)+(–588)×4 | |
| 69 | 21 | 3 | 6 | 26 | –15 | 6 = (–339)×26+(–588)×(–15) | |
| 21 | 6 | 3 | –85 | 3 = (–339)×(–85)+(–588)×49 | |||
| 6 | 3 | 2 | 0 – stop |
Ответ: 3 = (–339)×(–85)+(–588)×49, НОК(–339, –588) =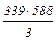 
= 66444.
3. Найти линейное разложение НОД(170, 588, 339).
Поскольку (170, 588, 339) = ((588, 339), 170) = (3, 170) = (170, 3), то вначале найдём линейное разложение (170, 3):
| Шаг | А | B | Q := A / B | R := A mod B | X | Y | Проверка |
| –1 | 0 | 1 | – | ||||
| 170 | 3 | 56 | 2 | 1 | –56 | 2 = 170×1+3×(–56) | |
| 3 | 2 | 1 | 1 | –1 | 57 | 1 = 170×(–1)+3×57 | |
| 2 | 1 | 2 | 0 – stop |
Таким образом, (170, 3) = 1 = 170×(–1) + 3×57.
Окончательно (используя предыдущий пример) получаем линейное разложение:
1 = (170, 588, 339) = (170, (588, 339)) = 170×(–1) + 3×57 =
= 170×(–1)+(588×(–49)+339×85)×57 = 170×(–1) + 588×(–2793) + 339×4845.
Дата добавления: 2021-12-14; просмотров: 284;
Поиск по сайту
Узнать еще
- Алгоритм анализа педагогической ситуации и решения педагогических задач.
- Алгоритм анализа последствий неадекватного поведения элемента на смежный с ним
- Алгоритм базовых реанимационных мероприятий (приложение 1)
- Алгоритм безопасного хэширования (Secure Hash Algorithm, SHA)
- Алгоритм Беллмана-Форда
- Алгоритм БПФ с прореживанием по времени
- Алгоритм ведения больных язвенной болезнью
- Алгоритм восстановления аналитической функции по её действительной или мнимой части.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
