Свойства делимости нацело

1⁰. Любое ненулевое целое число делится на единицу и на само себя (т.е. " a Î Z\ {0}1 | a Ù a | а).

Действительно, " a Î Za = 1×a, a = a×1.

2⁰. Отношение делимости нацело рефлексивно и транзитивно на множестве ненулевых целых чисел (т.е. " a Î Z \ {0} а | a и " а, b, c Î Z a | b Ù b | c ® a | c).

В самом деле, рефлексивность доказана в 1⁰, а транзитивность выводится просто: если b = a×n, c = b×m для некоторых целых m, n, то c = a×(n×m), где n×m – целое число, что и требовалось.

3⁰. Отношение делимости нацело антисимметрично на множестве натуральных чисел (т.е. " a, b Î N a | b Ù b | a ® a = b).

Действительно, если b = a×n, a = b×m для некоторых целых m, n, то, во-первых, m, n Î N, а во-вторых, b = (b×m)×n = b×(m×n), т.е. m×n = 1, и значит, m = n = 1, что и требовалось.

5⁰. Отношение делимости нацело не антисимметрично на множестве целых чисел, но " a, b Î Z a | b Ù b | a ® (a = b) Ú (a = –b).

Действительно, свойство антисимметричности нарушается, т.к. 1 | (–1) и (–1) | 1, но 1 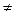–1. Тем не менее, аналогично предыдущему, если b = a×n, a = b×m для некоторых целых m, n, то b = b×(m×n), т.е. m×n = 1, и либо m = n = 1, либо m = n = –1, что и требовалось доказать.

6⁰. Если a | b , то для любого ненулевого целого c верно a | b×c, a×c | b×c, a×c | |b×c|, |a×c| | b×c.

Действительно, если b = a×n для некоторого целого n, то b×c = a×(n×c), b×c = (a×c)×n, |b×c| = ±(a×c)×n (в зависимости от знака b×c), и b×c = ±(a×c)×n (в зависимости от знака a×c),что и требовалось.

В частности, получаем

7⁰. Если a | b, то (±a) | (±b) при любой независимой друг от друга расстановке знаков у чисел a и b.

8⁰. Если a | b₁ , … , a | b_k , то a | (b₁ + … + b_k).

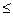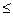В самом деле, если b_i = a×c_i для некоторых целых чисел c_i (1 i k), то b₁+ … +b_k = a×(c₁ + … + c_k) и c₁ + … + c_k – целое, что и требовалось.

9⁰. Если a | b₁ , … , a | b_k , то для любых целых c₁ , … , c_k верно a | (b₁×c₁+ …+b_k×c_k ) .

Это следствие 6⁰и 8⁰.

10⁰. Если a ¹ 0, b | a, то |b| £ |a|. В частности у каждого ненулевого целого числа лишь конечное число делителей.

В самом деле, если a = b×q (q Î Z), то |a| = |b|×|q|, и все числа в этом равенстве натуральные, так что |b| £ |a|. Таким образом,

b Î {–|a|, –|a| + 1, … , –1, 1, … , |a| – 1, |a|}

и поэтому у b может быть лишь конечное число значений.