Малые равнообъемные наклонения. Теорема Эйлера

Если на судно действует пара сил, вертикальных перемещений не будет, а возникнут только наклонения (крен или дифферент), которые называются равнообъемными, так как не будет наблюдаться изменение водоизмещения. Ватерлинии, соответствующие равнообъемным наклонениям, называются равнообъемными.

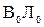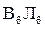Рассмотрим вначале крен судна (рис. 2.1) на бесконечно малый угол δθ. Так как и - равнообъемные ватерлинии, входящий объем 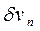и выходя-щий объем 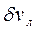равны между собой

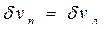. (2.1)

Объемы 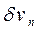и 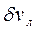можно определить как суммы элементарных призм с высотой yδθ и основанием ds :

;

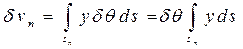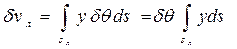, (2.2)

где s_п - площадь правой части ватерлинии; s_л - площадь левой части ватерлинии.

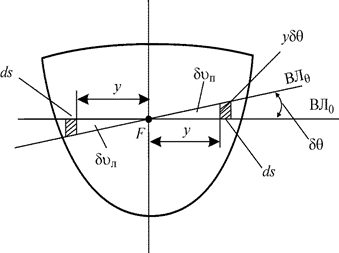
Рис. 2.1. Определение объемов и

Если учесть, что 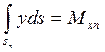- статический момент правой полуплощади ватерлинии относительно оси наклонения, параллельной оси Ох, а 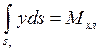- статический момент левой полуплощади, можно подставить (2.2) в (2.1) и получить

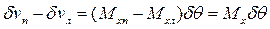, (2.3)

где М_х – статический момент площади всей ватерлинии относительно оси наклонения.

Но, так как левый и правый объемы равны друг другу, М_х = 0. Это возможно только в том случае, если ось, относительно которой вычислен момент М_х , проходит через центр тяжести площади ватерлинии .

Повторив эти же рассуждения для 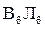, получим, что линия пересечения двух равнообъемных ватерлиний при бесконечно малом наклонении должна проходить через центры тяжести обеих ватерлиний. Это условие называется теоремой Эйлера. Теорема Эйлера верна для любого бесконечно малого наклонения (крена, дифферента).

Следствие из теоремы Эйлера.

Если повернуть плавающее судно на бесконечно малый угол относительно оси, проходящей через центр тяжести площади ватерлинии, то объем погруженной части судна не изменится.

Теорему Эйлера можно распространить и на конечные, но малые углы наклоне-ния. Предельная величина таких углов зависит от формы конкретного судна и от его загрузки. На практике считают углы малыми до 5 – 7 градусов. Для полностью погруженных судов теорема Эйлера справедлива вообще при любых углах наклонения.