Метацентры и метацентрические радиусы

Как было отмечено в предыдущем параграфе, касательная к траектории 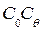в точке 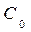параллельна 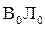, а в точке 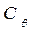- параллельна .

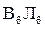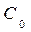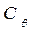Нормали, проведенные в точках и , пересекутся в точке М. Эта точка является центром кривизны дуги 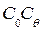, которая при малых углах наклонения станет дугой окружности радиуса r (рис. 2.3). Определяется r по формуле

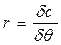, (2.10)

или с учетом (2.7)

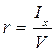. (2.11)

Величина r называется малым или поперечным метацентрическим радиусом, а точка М - поперечным метацентром. Так как 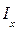и V - сугубо положительные числа, r всегда число положительное.

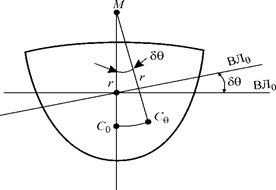
Рис. 2.3. Поперечный метацентр и поперечный метацентрический радиус

Рассуждая аналогично, получим радиус кривизны траектории С при продольных наклонениях:

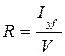. (2.12)

Этот радиус называется большим или продольным метацентрическим радиусом, а соответствующий центр кривизны - продольным метацентром (рис. 2.4).

С изменением осадки меняются 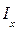, , 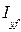V , следовательно, меняются также r и R . Примерный характер зависимостей r(z) и R(z) представлен на рис. 2.5. Эти кривые входят в комплекс кривых элементов теоретического чертежа.

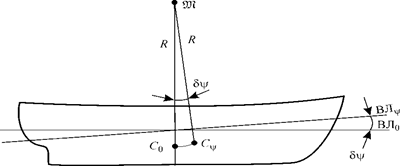
Рис. 2.4. Продольный метацентр и метацентрический радиусы

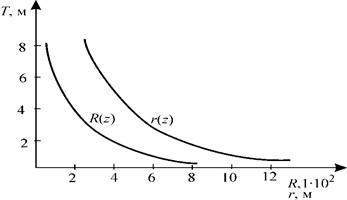
Рис. 2.5. Кривые метацентрических радиусов

Так как длина судна значительно больше ширины, момент инерции 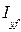значительно больше момента инерции 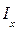, а R значительно больше r. Обычно R = L – 2L; r = 0,15 B – 0,30 B . Например, для прямоугольного понтона

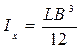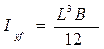; . (2.13)

Тогда

.

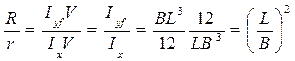Если L / B = 6, R / r = 36. Примерно такие же соотношения сохраняются и для судов.

Для полностью погруженного судна площадь ватерлинии равна нулю, т.е. моменты инерции и метацентрические радиусы равны нулю. Для цилиндри-ческого судна поперечный метацентр будет лежать на оси цилиндра, а траектория С при любых наклонениях будет круговой (рис. 2.6). Для шара поперечный и продольный метацентры будут совпадать с центром шара.

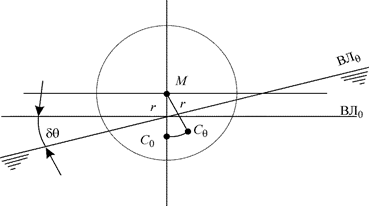
Рис. 2.6. Метацентр и метацентрический радиус для кругового цилиндра