Приближенные формулы для вычисления некоторых элементов плавучести

На начальной стадии проектирования часто необходимо рассчитывать мореходные качества в первом приближении. Для этих расчетов надо знать водоизмещение, координаты ЦВ и ЦТ судна, метацентрические радиусы и другие элементы.

Большая часть приближенных формул получена путем замены теоретических обводов судна математическими кривыми, в основном, параболами. Этот способ получения формул называется параболическим. Ряд формул получен при обобщении результатов практического проектирования.

На примере строевой по ватерлиниям рассмотрим параболический способ.

Заменим строевую по ватерлиниям параболой вида

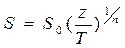, (1.110)

где в соответствии с рис. 1.38 :

S₀ - площадь ГВЛ ;

S – площадь ватерлинии при осадке z ;

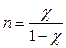- степень параболы ;

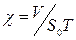- коэффициент вертикальной полноты судна.

После проведения всех выкладок получим формулу Эйлера для z_c

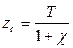. (1.111)

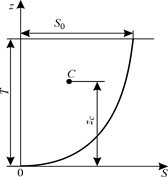
Рис. 1.38. Параболическая аппроксимация строевой по ватерлиниям

Аналогичным образом можно получить и некоторые другие формулы.

Приведем наиболее употребительные.

1. Для аппликат центра величины z_c :

а) формула Эйлера, которую мы получили выше

;

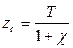б) формула Нормана (статистическая)

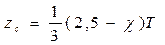; (1.112)

в) формула В.Г. Власова

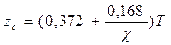; (1.113)

г) формула, также полученная с помощью параболической аппроксимации

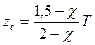; (1.114)

д) наиболее приближенная формула

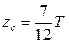. (1.115)

2. Для абсциссы центра величины х_с :

а) формула, полученная с помощью параболической аппроксимации отдельно носовой и кормовой ветвей строевой по шпангоутам

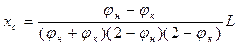, (1.116)

где 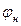- коэффициент полноты носовой ветви строевой по шпангоутам;

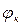- коэффициент полноты кормовой ветви;

б) формула Нормана (статистическая)

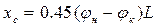; (1.117)

в) формула Хогга (статистическая)

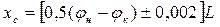, (1.118)

в которой при 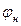> 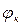следует брать знак минус, а при 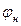< 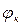- знак плюс.

3. Для абсциссы центра тяжести площади ватерлинии х_f :

а) формула, полученная при параболической аппроксимации отдельно носовой и кормовой ветвей ватерлинии

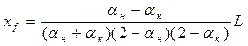, (1.119)

где 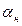- коэффициент полноты носовой ветви ватерлинии;

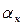- коэффициент полноты кормовой ветви;

б) формула Нормана (статистическая)

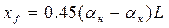. (1.120)

4. Для поперечного метацентрического радиуса:

а) формула И.А. Яковлева, полученная путем замены площади ватерлинии площадью особым образом подобранного прямоугольника

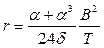, (1.121)

где α –коэффициент полноты всей площади ватерлинии; δ – коэффициент общей полноты судна;

б) формула Нормана (статистическая)

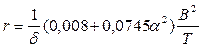; (1.122)

в) формула В.Г. Власова (упрощение параболической формулы)

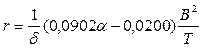. (1.123)

5. Для продольного метацентрического радиуса:

а) формула, полученная параболическим способом

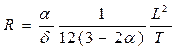; (1.124)

б) формула А.П. Фан-дер-Флита (упрощение формулы (1.124) с учетом статистики)

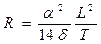; (1.125)

в) формула Нормана (статистическая)

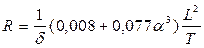; (1.126)

г) формула В.Г. Власова

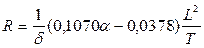; (1.127)

д) наиболее приближенная формула

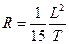. (1.128)