Бесконечно малые и их свойства
Определение. Функция 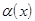 называется бесконечно малой в точке
называется бесконечно малой в точке  =
=  , если её предел в этой точке равен нулю,
, если её предел в этой точке равен нулю, 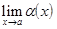 = 0. С помощью
= 0. С помощью  ,
, 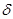 это можно записать так: "
это можно записать так: "  > 0 $
> 0 $ 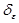 > 0 (
> 0 (  Î O (
Î O (  ,
, 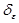 ) Þ |
) Þ | 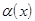 | <
| <  ).
).
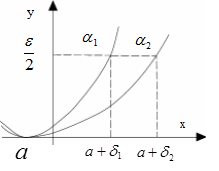
|
Теорема 1. Сумма конечного числа бесконечно малых функций есть функция бесконечно малая.
Доказательство. Докажем теорему для двух слагаемых 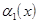 и
и 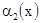 . По условию теоремы
. По условию теоремы
 <
< 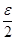 , если
, если 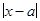 <
< 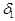 ,
,
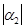 <
< 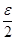 , если
, если 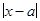 <
< 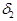 .
.
Пусть 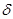 = min (
= min ( 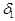 ,
, 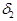 ), тогда
), тогда  <
< 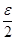 и
и 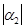 <
< 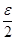 , если
, если 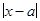 <
< 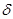 . Т.к. неравенствa одинакового смысла можно cкладывать, то имеем
. Т.к. неравенствa одинакового смысла можно cкладывать, то имеем  +
+ 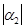 <
<  Þ
Þ 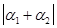 <
<  , если
, если 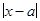 <
< 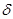 . Последняя запись означает, что
. Последняя запись означает, что 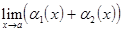 = 0. Теорема доказана.
= 0. Теорема доказана.
Теорема 2. Произведение бесконечно малой в точке  =
=  функции
функции 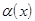 на ограниченную в этой точке функцию
на ограниченную в этой точке функцию 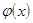 есть функция бесконечно малая.
есть функция бесконечно малая.
Доказательство. Запись $ 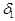 > 0, M > 0 (
> 0, M > 0 (  Î O (
Î O (  ,
, 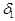 ) Þ
) Þ 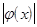 < M) означает, что функция
< M) означает, что функция 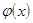 ограниченна в точке
ограниченна в точке  =
=  . Запись "
. Запись " 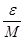 > 0 $
> 0 $ 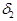 > 0 (
> 0 (  ÎO(
ÎO(  ,
, 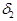 )Þ |
)Þ | 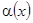 |<
|< 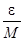 ) означает, что
) означает, что 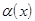 – бесконечно малая в точке
– бесконечно малая в точке  =
=  . В наименьшей из двух окрестностей точки
. В наименьшей из двух окрестностей точки  =
=  будут выполняться оба неравенства
будут выполняться оба неравенства 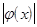 < M и |
< M и | 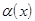 | <
| < 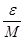 . Перемножая неравенства, получим |
. Перемножая неравенства, получим | 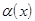 ×
× 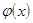 |<
|<  "
"  ÎO(
ÎO(  ,
, 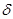 ),
), 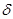 = min(
= min( 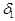 ,
, 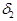 ). Последняя запись означает , что произведение
). Последняя запись означает , что произведение 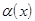 ×
× 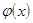 есть бесконечно малая в точке
есть бесконечно малая в точке  =
=  . Теорема доказана.
. Теорема доказана.
Теорема 3. Если 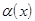 — бесконечно малая в точке
— бесконечно малая в точке  =
=  и не обращается в нуль в некоторой окрестности этой точки, то
и не обращается в нуль в некоторой окрестности этой точки, то 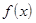 =
= 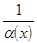 – бесконечно большая функция в этой точке. (Без доказательства).
– бесконечно большая функция в этой точке. (Без доказательства).
Дата добавления: 2020-02-05; просмотров: 734;











