Перемещение центра величины при малом равнообъемном наклонении

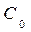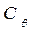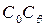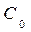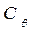При равнообъемных наклонениях, как было отмечено ранее, величина погруженного объема остается неизменной, но меняется его форма, вследствие чего изменяется положение центра величина (рис. 2.2) . Он перейдет из точки в точку по дуге . Секущая, соединяющая и при малом равнообъемном наклонении на угол 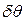, будет параллельна и пропорциональна перемещению ЦТ объемов 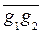, т.е.

;

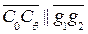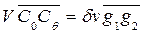. (2.4)

Определим объем элементарной призмы и отстояние ее ЦТ от ДП и 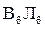. Они будут соответственно равны 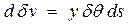(объем элементарной призмы); у (отстояние ее ЦТ от ДП ); 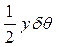(отстояние ее ЦТ от ).

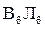Изменение статического момента от изменения формы подводного объема в результате добавления с правого борта объема будет равно

;

.

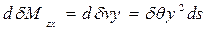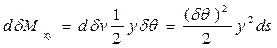Суммарное изменение статических моментов будет определяться по формулам

; ,

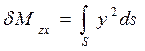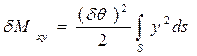а с учетом (2.4):

;

.

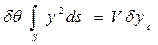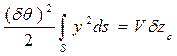Если ввести обозначение момента инерции площади ватерлинии относительно продольной оси, являющейся для нее и центральной

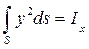, (2.5)

то получим

; ,

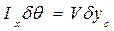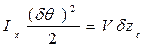откуда

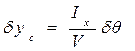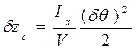; . (2.6)

Величина 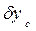- малая второго порядка, поэтому длина дуги кривой центров величины 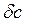будет равна

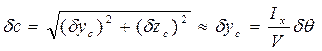. (2.7)

Отсюда следует, что касательная к траектории центров величины, проведенная через некоторую точку С, будет всегда параллельна плоскости ватерлинии, соответствующей точке С.

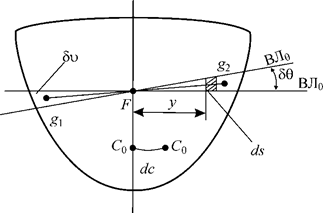
Рис. 2.2. Траектория перемещения ЦТ

Для наклонений в продольной плоскости получаются аналогичные формулы, т.е.

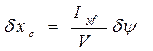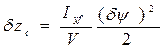; , (2.8)

где 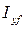- моментинерции площади ватерлинии относительно поперечной оси ff , проходящей через ее центр тяжести F (см. рис. 1.7);

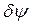- приращение угла дифферента.

Выражения для 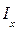и 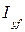были получены в разделе 1.9.