БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ
Основные теоремы о сходящихся последовательностях
1. Сходящаяся последовательность имеет только один предел.
2. Если последовательность сходится, то она ограничена.
3. Если две последовательности 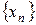 и
и 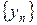 имеют пределы, равные
имеют пределы, равные 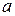 и
и 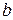 соответственно, то
соответственно, то
а) последовательность 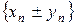 имеет предел равный
имеет предел равный 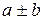 ,
,
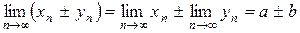
б) последовательность 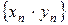 имеет предел равный
имеет предел равный 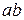 ,
,
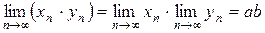
(постоянный множитель можно выносить за знак предела 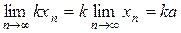 при любом постоянном
при любом постоянном 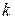 ).
).
В) последовательность 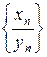 имеет предел равный
имеет предел равный 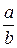
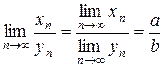 ,
,
при условии, что все 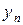 не равны нулю и
не равны нулю и 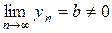 .
.
Пример.
Найти 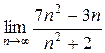 .
.
Решение.
Так как 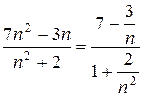 и
и 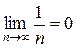 , то применяя теорему 3 в), получим
, то применяя теорему 3 в), получим
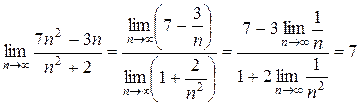 .
.
Примеры (для самостоятельного решения). Найти:
1. 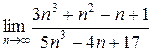 ; ;
| 2. 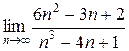 ; ;
|
3. 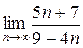 ; ;
| 4. 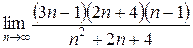 . .
|
Ответы:1) 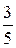 ; 2) 0; 3)
; 2) 0; 3) 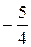 ; 4)
; 4) 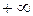 .
.
БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ
Если переменная величина 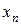 имеет своим пределом нуль
имеет своим пределом нуль 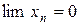 , то она называется бесконечно малой, или переменная величина
, то она называется бесконечно малой, или переменная величина 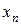 называется бесконечно малой, если для любого наперед заданного положительного числа
называется бесконечно малой, если для любого наперед заданного положительного числа 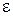 можно указать такое натуральное число
можно указать такое натуральное число 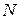 , что
, что 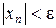 для всех номеров
для всех номеров 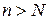 .
.
Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая.
Произведения ограниченной переменной величины на бесконечно малую есть величина бесконечно малая. Отсюда следует:
а) произведение постоянной величины на бесконечно малую есть также бесконечно малая величина;
б) произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая;
в) произведение двух бесконечно малых величин есть величина бесконечно малая.
Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая – оно может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной.
Переменная величина 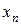 называется бесконечно большой, если, начиная с некоторого номера, она становится и остается при всех последующих номерах по абсолютной величине больше любого наперед заданного положительного числа
называется бесконечно большой, если, начиная с некоторого номера, она становится и остается при всех последующих номерах по абсолютной величине больше любого наперед заданного положительного числа 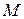 . Если
. Если 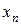 есть величина бесконечно большая, то записывается это так
есть величина бесконечно большая, то записывается это так 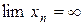 или
или 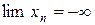 .
.
Обратим внимание, что из определения бесконечно большой величины следует, что знак 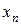 роли не играет, а требуется лишь чтобы абсолютная величина
роли не играет, а требуется лишь чтобы абсолютная величина 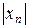 могла быть больше любого наперед заданного положительного числа. Символы
могла быть больше любого наперед заданного положительного числа. Символы 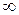 ,
, 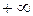 ,
, 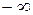 не являются числами, а лишь отражают тот факт, что переменная величина является бесконечно большой, поэтому никаких арифметических действий над этими символами производить нельзя.
не являются числами, а лишь отражают тот факт, что переменная величина является бесконечно большой, поэтому никаких арифметических действий над этими символами производить нельзя.
Бесконечно большая величина предела не имеет.
Если 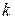 постоянная величина, не равная нулю
постоянная величина, не равная нулю 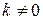 , то произведение
, то произведение 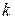 на бесконечно большую величину есть величина бесконечно большая.
на бесконечно большую величину есть величина бесконечно большая.
Произведение двух бесконечно больших величин есть величина бесконечно большая.
Отношение двух бесконечно больших величин не обязательно есть бесконечно большая величина, оно может быть величиной конечной, бесконечно большой и даже бесконечно малой.
Нельзя смешивать постоянное очень большое число с бесконечно большой величиной.
Например, функция 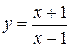 – бесконечно большая величина при
– бесконечно большая величина при 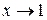 , при этом она стремится к
, при этом она стремится к 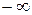 , если
, если  остается меньше 1, и стремится к
остается меньше 1, и стремится к 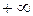 , если
, если  остается больше 1. А функция
остается больше 1. А функция 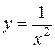 при
при 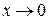 имеет пределом
имеет пределом 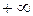 при любом изменении аргумента
при любом изменении аргумента  , стремящемся к нулю.
, стремящемся к нулю.
Бесконечно большие и бесконечно малые величины играют важную роль в математическом анализе. Между ними существует простая связь, хотя первые представляют собой функции, не имеющие предела, а вторые – функции, имеющие предел.
Если функция 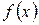 – бесконечно большая величина, то
– бесконечно большая величина, то 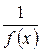 – бесконечно малая величина; если
– бесконечно малая величина; если 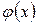 – бесконечно малая величина, то
– бесконечно малая величина, то 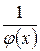 – бесконечно большая величина.
– бесконечно большая величина.
Важной для дальнейшего является следующая теорема:
Если функция 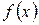 имеет предел
имеет предел 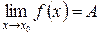 , то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины, т.е.
, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины, т.е. 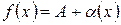 , где
, где 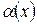 – бесконечно мала величина при
– бесконечно мала величина при 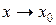 .
.
Функция 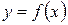 называется ограниченной в данном интервале, если существует такое положительное число
называется ограниченной в данном интервале, если существует такое положительное число 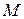 , что при всех значениях
, что при всех значениях  , принадлежащих этому интервалу, выполняется соотношение
, принадлежащих этому интервалу, выполняется соотношение 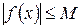 . В противном случае функция называется неограниченной.
. В противном случае функция называется неограниченной.
График ограниченной функции целиком лежит между прямыми 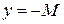 и
и 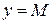 .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое бесконечно-малые величины?
2. Что такое бесконечно-большие величины?
3. Сформулируйте основные теоремы о сходящихся последовательностях.
4. Правило предельного перехода?
5. Определение предела функции?
6. Определение предела последовательности?
Дата добавления: 2021-09-25; просмотров: 985;











